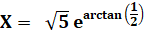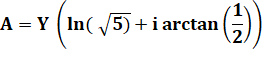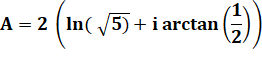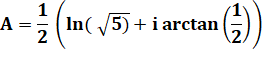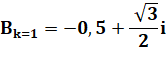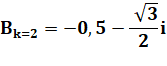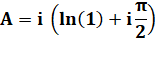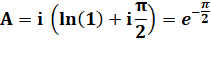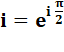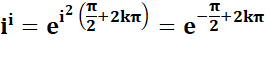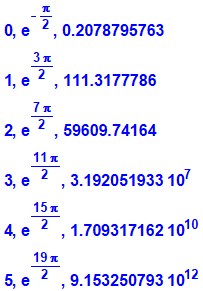NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/01/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres complexes
Débutants Complexes	PUISSANCE			Glossaire Complexe
INDEX Complexes Puissances	Réelle	Imaginaire	Complexe	Multi-valeurs
		Sommaire de cette page >>> Multi-valeurs de puissances complexes >>> Cas où Y est un rationnel – Carré et racine carrée >>> Cas où Y est un rationnel – Cube et racine cubique >>> Cas de 1 au carré >>> Cas de i puissance i >>> Théorème

Nombres complexes

MUTI-PUISSANCES

Il est habituel de proposer la racine carrée d'un nombre avec sa valeur positive, alors qu'il existe une valeur négative: ex: 4 = 2 x 2 = (-2) x (-2).

On retrouve un peu ce cas de figure pour les puissances complexes de nombres complexes.

Comment s'en rendre compte et les calculer ?
Examen du cas de i à la puissance i.

Voir Calculs ave i

Multi-valeurs de puissances complexes
Ce que nous allons montrer Un nombre complexe porté à une puissance prend plusieurs valeurs: Quantité finie si la puissance est réelle, ou Quantité infinie de valeurs si la puissance est complexe. Résultat qui conduit à déduire que la puissance de l'imaginaire peut prendre une infinité de valeurs.			Valeurs de: (a+ ib)^k => quantité finie (a+ ib)^(c+id) => quantité infinie i^i => quantité infinie Voir Le théorème
Pour le démontrer, passons le nombre complexe en polaire sous sa forme la plus générale, et prenons le logarithme.
Avec deux nombres complexes quelconques x et y. D'abord l'expression de cette puissance en exponentielle.
Transformation du log en forme polaire, vue ci-dessus.
Séparation des exposants de l'exponentielle => produit AB.
Soit un produit de deux termes:
Conclusion Puissances entre complexes:	X^Y = valeur classique x^y + valeur fonction de k, un relatif quelconque.

Exemple

X = 2 + i Y = 1 + 2i	X^Y = (2 + i)^(1 + 2i) = -0,425… + 0,775… i
X en polaire
Notre puissance
A
B selon la valeur de k un entier relatif
Z = X^Y = A.B

Cas où Y est un rationnel – Carré et racine carrée

Exemple du carré
=> valeur unique

X = 2 + i Y = 2	X^Y = (2 + i)^2 = 3 + 4i
A
B selon la valeur de k un entier relatif
Z = X^Y = A.B

Exemple de la racine carrée
=> deux valeurs en plus et en moins comme la racine carrée classique

X = 2 + i Y = 1/2	X^Y = (2 + i)^1/2 = 1,455…+ 0,3435… i
A	= 1,455…+ 0,3435… i
B selon la valeur de k un entier relatif
Z = X^Y = A.B

Cas où Y est un rationnel – Cube et racine cubique

Exemple du cube
=> valeur unique

X = 2 + i Y = 3	X^Y = (2 + i)^3 = 2 + 11i
A
B selon la valeur de k un entier relatif
Z = X^Y = A.B

Exemple de la racine cubique
=> trois valeurs en boucle

X = 2 + i Y = 1/3	X^Y = (2 + i)^1/3 = 1,292…+ 0,201… i
A	= 1,292…+ 0,201… i
B selon la valeur de k un entier relatif
Z = X^Y = A.B

Cas de i^2

Exemple du carré
=> valeur unique

X = i Y = 2	X^Y = i² = - 1
A
B selon la valeur de k un entier relatif
Z = X^Y = i^2 = A.B

Exemple de la racine carrée
=> trois valeurs en boucle

X = i Y = 1/2	X^Y = (i)^1/2 = 0,707… + 0,707… i
A	= 0,707… + 0,707… i
B selon la valeur de k un entier relatif
Z = X^Y = i^1/2 = A.B

Ca où X = i et Y = i

Exemple du carré
=> valeur unique

X = i Y = i	Z = X^Y = i^i = 0,27879576…
A
B selon la valeur de k un entier relatif
Z = X^Y = i^i = A.B

Approche plus directe dans ce cas.

On retrouve bien les valeurs de Z = iⁱ

Généralisation de:
Calcul de i^i
Formule de Moivre
Valeurs de Z = i^i selon k

Merci à Denis Archambaud pour avoir proposé cette approche directe

Théorème

Retour	Puissance de l'imaginaire
Suite	Puissance complexe Complexes – Index
Voir	Constantes Construction de l'heptagone Inventaire des types de nombres Nombre de Gauss Nombres – Glossaire et index Nombres d'Eisenstein Nombres périodiques Nombres réels Puissances et racines – Index
Site	Complex exponentiation – Wolfram MathWorld Complex number to a complex power may be real – Cut-The-Kont Complex power of a complex number – Mathematics Raising a Number to a Complex Power – University of Toronto Complex Power Functions – Mathonline
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/PuisImMu.htm