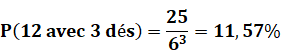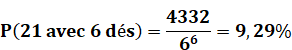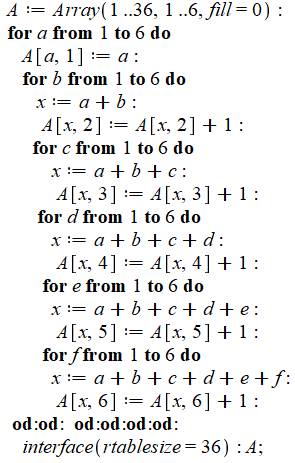|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
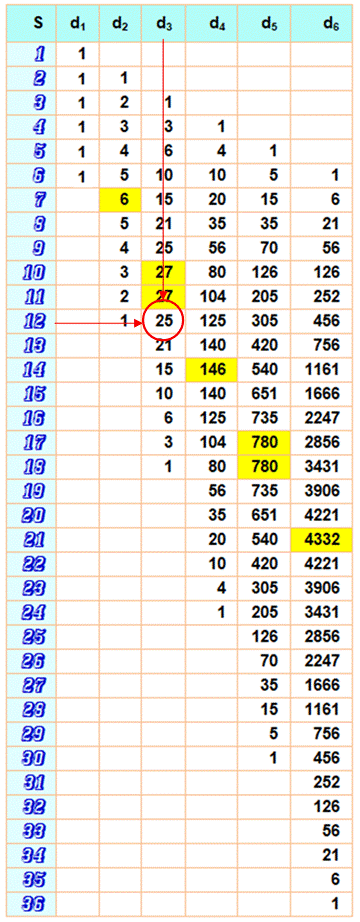
Avec UN à SIX dés Combien de fois atteint-on
le nombre k avec 1, 2, 3, 4, 5 ou 6 dés ? Table et programmes. |
Voir Sommes
avec deux dés – Détail
|
|
||
|
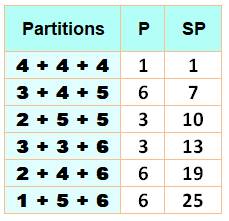
Combien
de possibilités d'avoir la somme 12 avec trois dés ? Un
décompte simple (aidée éventuellement d'un tableur) montre qu'il y a 25 cas. (Tableau =>) Une autre
manière consiste à trouver les tri-partitions
de 12 avec trois nombres inférieurs à 7:
|
|
|
|
|
||
|
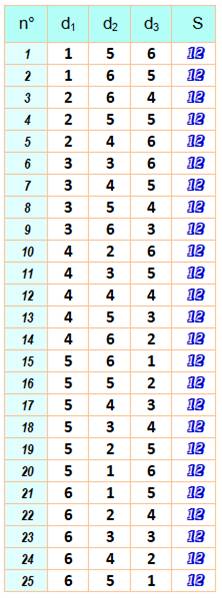
Lecture Exemple avec la somme 12 (en rouge) On retrouve la somme 12 vue ci-dessus obtenue 25 fois
avec trois dés (d3). On a aussi la somme 12 une seule fois avec deux
dés (6 + 6). Exemple avec la somme 10 Elle est obtenue:
Somme des colonnes La somme sur
chaque colonne est égale à toutes les possibilités de jeu avec k dés. Calcul de probabilité Comme
d'habitude la probabilité
est égale au nombre de cas favorables sur la quantité totale des cas. Exemples
Fonctions génératrices Il existe des polynômes donnant
toutes ces valeurs >>> |
|
|
Merci à François Lessard pour l'amélioration
de ce tableau
|
|
||
|
|
Commentaires Déclaration d'une matrice (Array) de 36 lignes et
6 colonnes dont toutes les valeurs sont mises à 0. La méthode directe consiste à explorer les dés
les uns après les autres. Avec le premier dé (boucle en a), on remplit la
colonne1, avec le deuxième dé (boucle en b), on remplit la deuxième colonne,
etc. Pour chaque valeur, on ajoute 1 à la case
correspondante de la matrice.
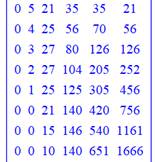
Avec print(A), le programme indique la nature de
la matrice. Pour visualiser le contenu, il faut double-cliquer dessus. Extrait de la matrice
calculée. |
|
Voir Programmation – Index
|
|
||
|
|
Commentaires Procédure qui calcule le nombre de cas où la
somme atteint n pour k dés. Appel des logiciels de combinatoire. Partitions de n placées dans P. Premier tri: on ne conserve que les partitions
ayant k éléments. Deuxième tri: on élimine toutes les partitions
avec un terme supérieur à 6. On identifie ce cas avec t = 0. Alors, si la partition est retenue (t = 1), on calcule
la quantité de permutations qui est ajoutée au cumul S. Exemple d'appel à la procédure avec la quantité
de fois que le total est égal à 21 pour six dés: 4 332. . |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()