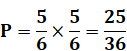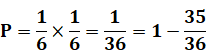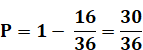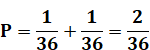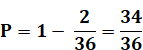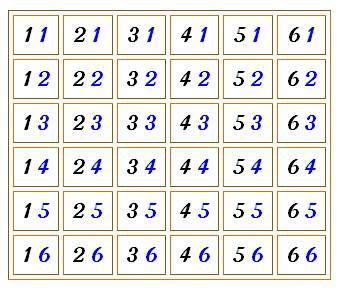
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/04/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Maths et hasard
Débutants Statistiques	PROBABILITÉS & Statistiques				Glossaire Probabilités
INDEX Grands nombres Dénombrement	Jeu de dés		Deux dés	Double Six
	Dénombrement		Trois dés	Probabilités et Dés
	Table 1 à 6 dés		Trois dés et une urne	Proba. mêmes chiffres
		Sommaire de cette page >>> Probabilités avec un seul dé >>> Possibilités avec deux dés >>> Tirage du 6, du double-6 >>> Autres cas >>> Anglais

Avec DEUX dés

Quelles sont toutes les possibilités en lançant un dé deux fois de suite ou en lançant deux dés à la fois.

Apprendre les probabilités très simplement avec les dés.

Rappel avec un dé

En lançant un dé (non pipé) des centaines de fois, je constate que chacun des six nombres sort autant de fois. On dit que la probabilité d'avoir le 1 (par exemple) est de 1/6. La probabilité est le rapport des cas favorables (ici un seul) sur la totalité des cas possibles (ici 6). La probabilité est donc de 1/6 = 0, 1666… ou encore 16, 666…%. La probabilité d'avoir un quelconque nombre autre que le 6 est calculée de la même manière: il y a 5 cas où ce n'est pas le 6 sur un total de 6 possibilités, soit une probabilité de 5/6 = 0, 8333… = 83, 333…% Il est important de noter que la somme des probabilités d'avoir un 6 ou de ne pas l'avoir est égale à 1 (1/6 + 5/6 = 1). La probabilité égale à 1 est celle de la certitude: il y a 6 chances sur 6 que le dé tombe sur un nombre. À l'inverse, il y a 0 chance sur 6 pour que le dé tombe sur un nombre autre que 1, 2, 3, 4, 5 ou 6. La probabilité est nulle. Comme nous le verrons, dans certains cas, il est plus facile de passer par le calcul de la probabilité de l'événement contraire. 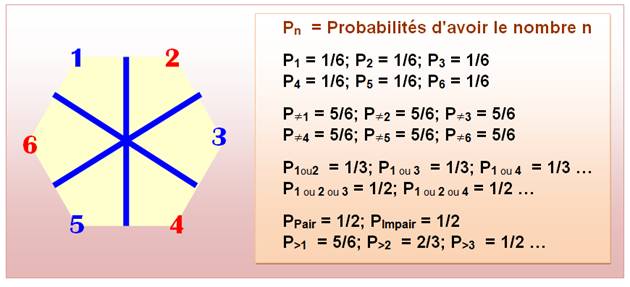Résumé des probabilités avec le lancer d'un seul dé

Toutes les possibilités avec deux dés
Le tableau à double-entrée montre les 36 = 6 x 6 possibilités La somme des deux dés varie de 2 à 12. Il y autant de somme paires et de sommes impairs (18+ 18 = 36) Le produit des deux dés varie de 1 à 36. Il y a 27 produits pairs (27 = 3 x 6 + 3 x 3) et 9 produits impairs.

Voir Somme donnée avec deux dés / Avec trois dés

Avec le 6 (ou un autre nombre)
En jaune les cas favorables selon ce que l'on cherche:
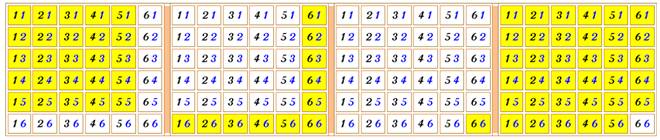
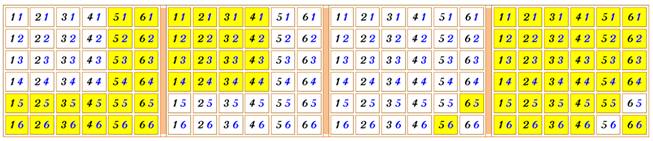
Aucun 6	Au moins un 6	Deux 6	L'un n'est pas 6
5 x 5 = 25	6 + 6 – 1	1	6 x 6 – 1
25 / 36	11 / 36	1 / 36	35 / 36
Aucun 6 Avec un dé, il existe cinq possibilités de ne pas avoir un 6. Avec le second dé, et pour chacun des cas du premier dé, il y aura cinq possibilités de ne pas avoir un 6. Soit 25 possibilités au total. Soit une probabilité de 25/36 = 0,69444… = 69,444…% Au moins un 6 Avec un dé, il existe 6 possibilités d'avoir 6. Avec le deuxième dé, il existe 6 autres possibilités, dont une en commun avec le premier dé (66). Soit un total de 11 et une probabilité de 11/36 = 30,555…% Deux 6 Il n'y a qu'une seule configuration donnant le double-six. Probabilité: 1/36 = 2,777…% L'un des deux dés n'est pas un 6 Dans tous les cas, sauf évidemment, si les deux dés sont 6. Probabilité: (36 – 1)/36 = 35/36 = 97,222…%

Autres cas
5 ou 6	pas de 5 ou 6	5 et 6	pas de 5 et 6
36 – 4 x 4	4 x 4	2	36 – 2
20/36 = 5/9	16/36 = 4/9	2/36 = 1/18	34/36 = 17/18
Pas de 5 ou 6 (ou tout autre couple de nombre) Avec un dé, il existe quatre possibilités de ne pas avoir un 5 ou un 6. Avec le second dé, et pour chacun des cas du premier dé, il y aura quatre possibilités de ne pas avoir un 5 ou un 6. Soit 16 possibilités au total. Soit une probabilité de 16/36 = 4/9 = 0,444… = 44,444…% 5 ou 6 Événement contraire du précédent: 5 et 6 ou faire un total de 11 points Dénombrement facile: 2 cas. Ou, on peut dire: Si j'ai un 5 (probabilité 1/6), il y a une chance sur 6 d'avoir un 6, soit probabilité de 56 = 1/36. Et, si j'ai un 6 (probabilité 1/6), il y a une probabilité de 1/6 d'avoir un 5, soit probabilité de 56 = 1/36. Ces deux cas étant bien indépendants (exclusifs), la probabilité des deux et la somme des probabilités. Pas 5 et 6 Événement contraire du précédent:

ENGLISH CORNER

We assess the chances of winning a gamble in which we throw a single die once. There are 6 possible outcomes of such a roll, namely one of the numbers: 1, 2, 3, 4, 5, 6. If each of these outcomes is equally likely (as is the case for a true die), you will win one out of 6 times by betting on rolling a specified number. The probability of one dice not being a particular number is 5/6. The probability of two dice not being a that number is 5/6 x 5/6 = 25/36. The sum of points 10 can be made up by 27 different dice-throws, but the sum of points 9 by 5 only. >>> The singular of dice is die. But, the form dice, used as plural and singular, is of much more frequent occurrence in gaming and related senses than the singular die.

Suite	Trois dés
Voir	Dénombrement Échecs Jeux – Index Jeux de hasard (loto, tiercé …) Pentominos Probabilités Trois pièces
DicoNombre	Nombre 3 Nombre 36
Site	Throwing dice - theory (interactif)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Probabil/DesTrois.htm