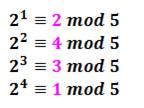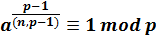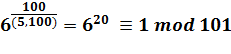|
||||||||||||||||||||||||||||||||||||||||
![]()
|
ORDRE MULTIPLICATIF RACINE PRIMITIVE Notion
de la théorie des nombres faisant intervenir la congruence des puissances
d'un nombre modulo un autre. Avant
de partir vers plus d'abstraction, il est utile de bien comprendre ces deux
notions à partir d'exemples. |
Anglais:
multiplicative order / primitive root
Rappels
|
Nombres premiers entre
eux: aucun facteur commun – Notés (a, b) = 1 Indicatrice
d'Euler (ou totient): quantité de premiers avec m et inférieurs à m –
Notée Congruence de
a modulo m: reste de la division de a par m; on dit résidu et on note:
|
|
|
||
|
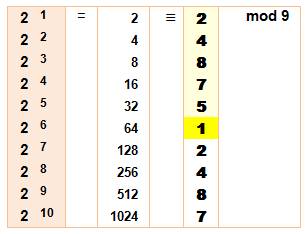
Prenons
deux nombres premiers entre eux: 2 et 9. Calculons
les puissances successives du premier nombre (2), et leur reste dans la
division par le second nombre (modulo 9). Nous observons
que les restes suivent une périodicité: 2, 4, 8, 7, 5 et 1. L'exposant ( = 6) pour lequel le modulo de la puissance
vaut 1 est défini comme l'ordre multiplicatif
de 2 modulo 9. On dit aussi parfois que 2 appartient à l'exposant 6 modulo 9. Ainsi,
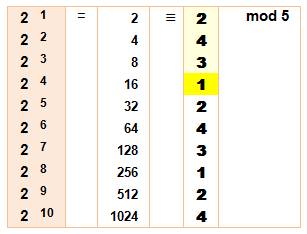
tableau du bas, l'ordre multiplicatif de 2 modulo 5 est 4. Dans ce
cas, notez que la période est 4 (= 5 – 1) et que tous les restes possibles
(de 1 à 4, sauf le 0) font partie de la période. On dit,
dans ce cas, que 2 est une racine primitive
modulo 5 |
L'ordre
multiplicatif de 2 par rapport à 9 est 6. Plus petit exposant tel que 2k
divisé par 9 produit un reste égal à 1.
L'ordre
multiplicatif de 2 par rapport à 5 est 4. Le
nombre 2 est une racine primitive modulo 5 car, avec les puissances
précédentes nous avons eu tous les restes possibles. |
|
Analyse
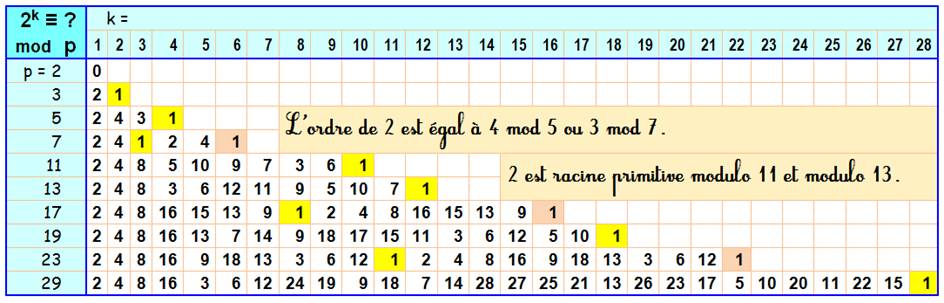
des puissances premières de 2
|
Lecture:
pour p = 7 et k = 3, 23 = 8
qui est congru à 1
mod 7; c'est la plus petite puissance pour laquelle le résidu vaut 1. La
puissance 3 est l'ordre de 2 modulo 7. Notez que pour 5, 11, 13, 19 et 29,
la ligne comporte tous les restes possibles de la division par ce nombre. 2
est une racine primitive de tous ces nombres premiers. L'ensemble de tous les
restes est nommé: classe des résidus
modulo p. Remarque: la classe des résidus ne
contient par le 0. En effet, 2 et p sont premiers entre eux. Une puissance de
2 ne peut pas être divisible par p. |
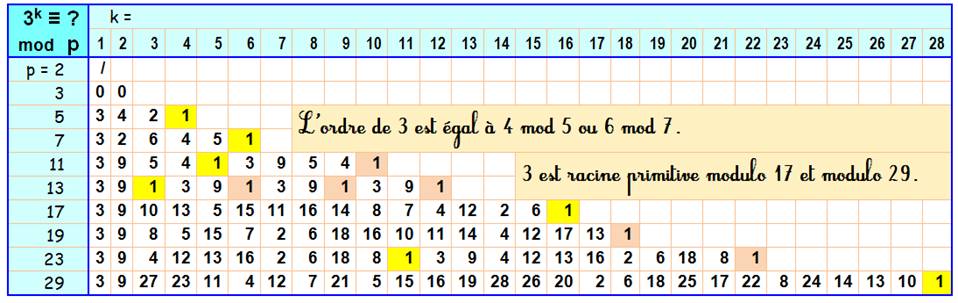
Analyse
des puissances premières de 3
|
Lecture:
pour p = 7 et k = 6, 36 = 32
x 32 x 32 ≡ 2 x 2 x 2 ≡ 8 ≡ 1 mod 7 ; c'est la plus petite puissance pour
laquelle le résidu vaut 1. La puissance 6 est l'ordre de 3 modulo 7. De plus,
tous les résidus ont été balayés. On remarque que k = 6 = 7 – 1. Le nombre 3
est racine primitive du nombre premier 7. Pour p = 13, la longueur du cycle
des résidus est 3 au lieu de 12, si on avait affaire à une racine primitive.
Mais, et c'est une propriété, 3 est un diviseur
de 12. |
|
|
||
|
Définition Soit m un entier positif et a un entier
quelconque, avec a et m premiers entre eux. Soit k le plus petit entier tel que: a puissance k est congru à 1.
L'exposant k est appelé ordre
(multiplicatif) de a modulo m. Définition mathématique Soit m L'ordre
de a modulo m est l'entier k tel que:
|
(a,
m) = 1
ordm(a) = k
ord9(2) = 6
ord5(2) = 4 |
|
|
Propriétés L'ordre
multiplicatif k est toujours inférieur à m ( démonstartion avec le petit théorème
de Fermat). La valeur
de k est au plus égale à l'indicatrice
d'Euler (théorème
d'Euler). Si (a, m)
= 1, alors k divise Phi (m). Si m est
premier, alors k est un diviseur de Phi (p) = p – 1. |
|
|
|
|
||
|
Définition On dit
que a est une racine primitive modulo m si l'ordre de a est égal à Phi (m). C'est-à-dire
si Phi (m) est effectivement le plus petit exposant pour lequel le résidu
vaut 1. |
|
|
|
Propriétés Chacune
de racines primitives forme un système réduit de résidus. Si m est un nombre
premier la classe des résidus est complète. Dit
autrement: avec un nombre premier p,
l'ordre vaut p – 1 et tous les restes possibles précédent cette
puissance. |
|
|
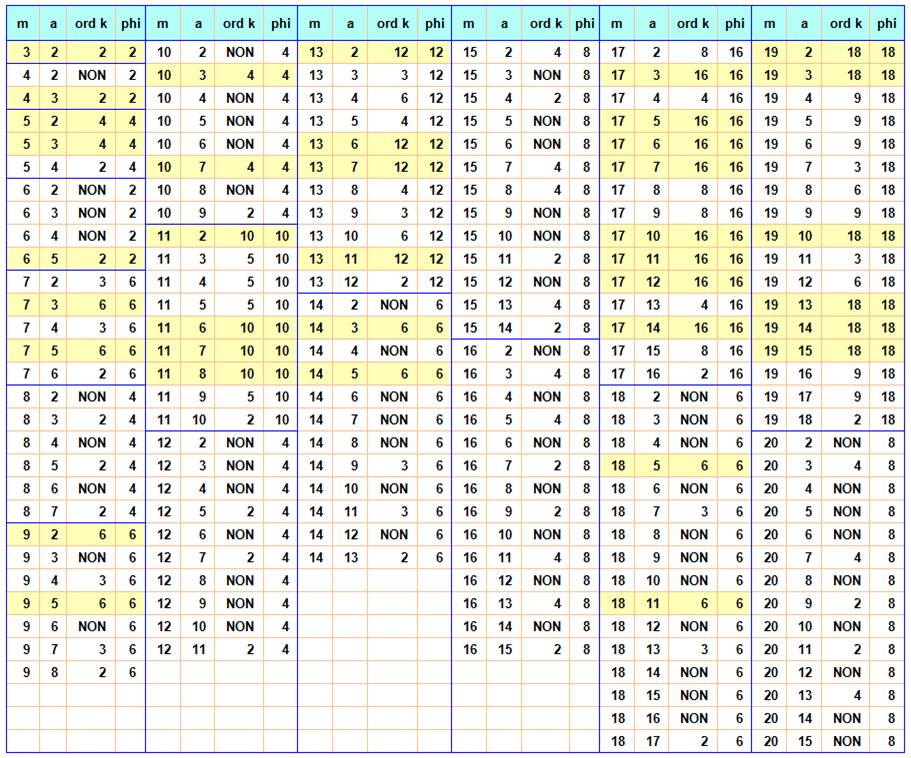
Tableau de comparaison entre ordre et phi
|
Lecture:
On calcule k le plus petit, tel que ak
congru à 1 modulo m et on compare à la valeur de Phi (m). En jaune, les cas
où il y a égalité entre l'ordre et Phi. On se souvient que Phi (p) = p – 1. La ligne avec un Non, indique
qu'aucun résidu égal à 1 ne peut être trouvé pour cette configuration. |
|
|
|||
|
Tout
premier p possède Phi (p – 1)
primitives |
Dans le tableau ci-dessus, la quantité de ligne jaune pour un nombre
premier est égale à Phi du nombre précédent. Ainsi 17 compte 8 lignes jaunes (8 racines primitives) et Phi (16) =
8. |
||
|
Si m
n'est pas premier, les racines primitives n'existent que si => |
m = (2, 4, ou pk ou 2pk) avec p premier impair |
||
|
Si a est
d'ordre k modulo m, alors l'ordre de a puissance h est égal à k / (k, h) |
Ord5 (3) = 4 Ord5 (32) = 4 / (4, 2) = 4 / 2 = 2 Ord7 (3) = 6 Ord7 (311) = 6 / (6, 11) = 6 / 1 = 6 |
||
|
Si a est
d'ordre k modulo m et si b est d'ordre
h modulo m et si (k, h ) = 1, alors ab est d'ordre hk modulo m. |
Ord5 (2) = 4 Ord5 (3) = 4 Ord5 (6) = 16 |
||
|
Soit les entiers
naturels m et n. Les propositions suivantes sont équivalentes:
|
(m, n) = 1
|
||
|
Si p est
premier et (a, p) = 1, alors
possède
(n, p – 1) solutions à condition que:
Et aucune
solution sinon. |
x5 Test d'existence de solution:
En effet, en mod 101 Quantité de solutions: (5, 100) = 5 Un calcul donnerait ces cinq solutions: x |
||
|
|
|
|
Let m denote a positive integer and a any integer such that (a, m) =
1. Let k be the smallest positive integer such that |
|
![]()
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/ARITHMET/RacinPri.htm
|
![]()