NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/05/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	DIVISIBILITÉ
Débutants Division	Suite de nombres			Glossaire Division
INDEX Divisibilité	Général	Suite	Paire
		Sommaire de cette page >>> Théorème >>> Démonstration >>> Analyse des cas >>> Théorème alternatif

Ensemble de NOMBRES

contenant une paire divisible

Combien de nombres sont-ils nécessaires dans un ensemble pour qu'il existe au moins une paire divisible: l'un divisant l'autre?

De manière équivalente: une paire de multiple, l'un est multiple de l'autre.

Divisibilité dans un ensemble de n+1 nombres
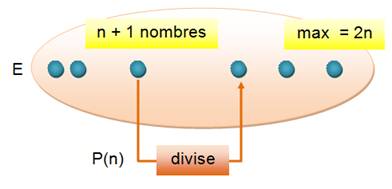
Démontrer que: Dans un ensemble de n+1 entiers, aucun plus grand que 2n, il y a toujours au moins un nombre qui en divise un autre. Exemple avec n = 4 Soit 5 nombres inférieurs ou égaux à 8. Je choisis, par exemple, les quatre premiers {2, 3, 5, 7}. Reste pour le cinquième: 1, 4, 6 ou 8. Quel que soit mon choix, il y aura toujours un couple se divisant.	Ensemble E de n + 1 nombres entiers, le plus grand est 2n. La proposition P(n) dit qu'il existe toujours un nombre qui en divise un autre.
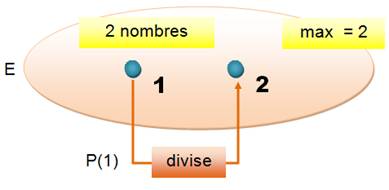
C'est vrai pour n = 1. Parmi les deux seuls nombres de l'ensemble, le nombre 1 divise bien 2.
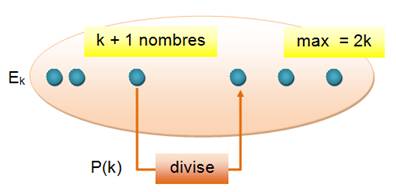
Supposons que la proposition soit vraie pour n = k. Oui! C'est la même figure en remplaçant n par k. Mais cela signifie que nous avons choisi un nombre particulier k (et non pas n'importe lequel n). Nous avons instancié la proposition. Subtilité de mathématicien!
Il faut démontrer qu'avec notre supposition, la proposition est également vraie pour k+1, le nombre suivant k; que la proposition est héréditaire. Remarquons qu'en passant de Ek à Ek+1, nous ajoutons un élément à l'ensemble; et parmi tous les éléments, deux peuvent dépasser la précédente borne: 2k+1 et/ou 2k+2.	Tout repose sur l'existence ou non des nombres 2k+1 ou 2k+2.

1) Si le nouvel ensemble Ek+1 ne contient aucun élements débordant:	Alors nous avons strictement l'ensemble Ek et notre proposition étant vraie pour k elle l'est pour k + 1.
2) Si le nouvel ensemble contient un seul élément débordant: 2k+1 ou 2k+2	Alors cet élément peut être considéré comme l'élément ajouté à l'ensemble Ek. Ce qui signifie que Ek est conservé dans sa définition (même si ce ne sont pas les mêmes éléments). Notre supposition s'applique pour Ek et donc pour Ek+1.
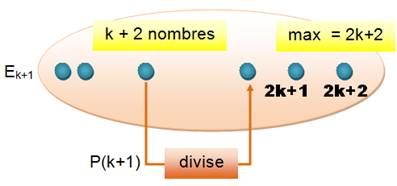
3) Si le nouvel ensemble contient les deux éléments débordants 2k+1 et 2k+2 31) Si k+1 est dans Ek+1	Le nombre k + 1 divise 2k + 2 = 2(k + 1). La proposition est vraie.
32) Si k+1 n'est pas dans Ek+1 Nous l'ajoutons à l'ensemble Ek+1, et nous retirons 2k+2. Nous venons de créer un nouvel ensemble "artificiel" pour le besoin de la démonstration.	Cet ensemble artificiel comporte toujours k+2 nombres et le plus grand est inférieur à 2k+2. Il répond à notre définition. Il a un seul élément débordant 2k+1. C'est l'ensemble du cas 2). La proposition P(k+1) est donc vraie aussi dans ce cas.
La proposition P(n) est vraie pour n = 1, et elle est vraie pour P(k+1) dès qu'elle vraie pour P(n) …	Alors, par induction, la proposition P(n) est vraie pour tous les entiers.

Théorème équivalent

En passant de n+1 à n, il est équivalent de dire:

Parmi n nombres entiers pris au hasard, pour obtenir une paire de nombres divisibles, il suffit que le plus grand ne dépasse pas 2n-2.

Suite	Divisibilité d'une somme Formes diverses Critères généraux Divisibilité – Index
Voir	Calcul mental – Index Fermat n nombres divisibles par n Principe des tiroirs et divisibilités Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/aaaDIVIS/PairDivi.htm