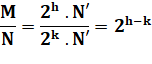Divisibilité dans une suite de nombres

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/04/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	DIVISIBILITÉ
Débutants Division	Suite de nombres			Glossaire Division
INDEX Divisibilité	Général	Suite	Paire
INDEX Divisibilité		Sommaire de cette page >>> Approche >>> Recherche de la suite maximale

SUITE de NOMBRES

Parmi les premiers nombres, peut-on trouver une suite dont aucun n'est divisible par un autre?

Approche

Parmi les dix premiers nombres, il existe diverses possibilités pour en choisir u certain nombre tels que nul ne divise un autre.

Sur le tableau:

¹ ces nombres sont tous premiers entre eux;

² certains nombres de ces nombres ont des facteurs communs, mais ne sont pas divisibles. Ex: 4 et 6 sont divisibles par 2 mais 4 ne divise pas 6.

³ cette suite est la plus petite des plus grandes avec cinq termes.

Recherche de la suite maximale
Un nombre peut s'écrire sous la forme d'un produit d'une puissance de 2 et d'un nombre impair.		N = 2^k . N'_Impair
Si deux nombres ont même facteur impair N'. Supposons que h > k , sinon, on inverse. M est divisible par N; le quotient est une puissance de 2.		N = 2^k . N'_Impair M = 2^h . N'_Impair
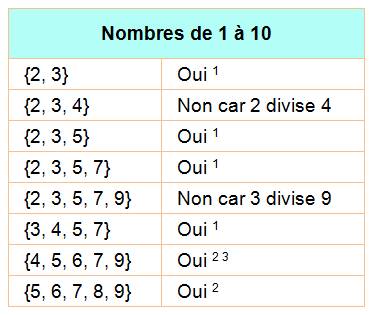
Pour avoir une suite de non-divisible, il faut donc que tous les N' des nombres choisis soient différents		Ex: pour les nombres de 1 à 100, il y a 50 nombres impairs tous différents. Dans ce cas, la suite maximale ne peut pas excéder 50 termes. Et, à l'inverse, toute suite de 51 termes ou plus contiendra au moins deux nombres divisibles l'un par l'autre.
Conclusion	Parmi n + 1 nombres choisis parmi les 2n premiers nombres, il y en aura toujours au moins un qui en divisera un autre. En choisissant les nombres {n+1, n+2, …2n} vous êtes sûr d'avoir une suite telle qu'aucun n'en divise un autre.
Premiers entre eux	Deux nombres consécutifs sont premiers ente eux. En ajouter un troisième ne garantit pas que les trois soient premiers entre eux. Notamment, il peut y avoir deux pairs.

Suite

Voir

Cette page