|
|||||||||||||||||||||||||||||||||||
![]()
|
Nombres divisibles par tous les nombres de 1 à k sauf pour deux consécutifs Recherche de tels nombres
selon la valeur de k. Parfois occasion de poser une
énigme. |
|
|
|||
|
Considérons le nombre 6 |
6 / 1 = 6 6 / 2 = 3 6 / 3 = 2 6 / 4 = 3/2 6 / 5 = 6/5 6 / 6 = 1 |
Le nombre 6 est divisible par
tous les nombres jusqu'à 6, sauf par 4 et 5, deux nombres consécutifs. Le nombre 6 répond à notre
recherche pour k = 6. |
|
|
Considérons le nombre 42 |
42 / 2 = 21 42 / 3 = 14 42 / 4 = 21 / 2 42 / 5 = 42 / 5 42 / 6 = 7 42 / 7 = 6 |
Le nombre 42 est divisible par
tous les nombres jusqu'à 7, sauf par 4 et 5, deux nombres consécutifs. Le nombre 42 répond à notre
recherche pour k = 7. Le suivant ayant ces mêmes propriétés est 126 = 3 x 42. Le facteur 3 conserve les divisibilités
et les non-divisibilités par 4 et 5. |
|
|
Général |
Comment s'y prendre pour trouver
ces nombres pour k de plus en plus grand ? |
||
|
|
||||
|
Notre but On
cherche un nombre N dont on sait qu'il est divisible par tous les nombres de
1 à 10, à l'exception d'exactement deux nombres consécutifs. Lesquels,
et valeur(s) de N ? |
Si N était divisible par tous les nombres ce serait au moins le plus petit commun
multiple des nombres de 1 à 10: PPCM (1 à 10) = 2 520 = 23 . 32 . 5 . 7 Avec une sélection parmi ces facteurs
on peut recréer tous les nombres de 1 à 10. |
|||
|
Cas du nombre maximum 10 qui impose
que N est nécessairement divisible par les petits nombres. |
Supposons que N ne soit pas divisible par 2, alors N n'est pas
divisible par tous les nombres pairs (2, 4, 6, 8 et 10); cinq non-divisibilités. Plus que les deux demandées. Il est nécessaire que N soit divisible par 2. Supposons que N ne soit pas divisible par 3, alors N n'est pas
divisible par les multiples de 3 (6, et 9); trois non-divisibilités. C'est la
quantité correcte, mais pas les nombres ne sont pas consécutifs. N est divisible par 3. … idem pour 4 et 5. Avec la divisibilité par 6, son multiple 12 dépasse la valeur maximale
10. Pas de conclusion possible pour 6. Mais on a déjà
éliminé tous les nombres de 1 à 5. La double
non-divisibilité se trouve au-delà. |
|||
|
Valeur minimale de N qui est
divisible par tous les nombres de 1 à 5 |
N est divisible par, au moins, tous les nombres de 1 à 5, donc par le
plus petit commun multiple de ces nombres: Nmin = PPCM (1 à 5) = 60 = 22 . 3 . 5 |
|||
|
Tri des nombres de 6 à 10 selon la
divisibilité de 60 par ces nombres |
Parmi les nombres de 6 à 10 certains divisent naturellement le nombre
Nmin = 60 (notés en rouge): [6, 2 x 3], [7,
7], [8, 23], [9, 32], [10, 2 x 5] |
|||
|
Conséquences, par élimination |
Seuls trois nombres (7, 8 et 9) sont rescapés et la double non-divisibité
doit se trouver parmi eux avec (7 ,8) ou (8, 9) comme couples consécutifs. |
|||
|
Deux couples candidats et deux
solutions: |
Avec (7 et 8), en multipliant Nmin par 7, on conserve la non-divisibilité pour
les deux nombres consécutifs (8 et 9) N = 60 x 7 = 420,
divisible par les nombres de 1 à 10 sauf 8 et 9. Avec (8 et 9), en multipliant Nmin par 3, on crée la divisibilité par 9 tout en
conservant la non-divisibilité pour les deux nombres consécutifs (7 et 8) N = 60 x 3 = 180,
divisible par les nombres de 1 à 10 sauf 7 et 8 |
|||
|
Valeur des quotients de N par 1 à
10, dans les deux cas, en guise de vérification |
[1, 180], [2, 90], [3, 60], [4, 45], [5, 36], [6, 30], [7, 180 / 7], [8, 45 / 2], [9, 20], [10, 18] |
[1, 420], [2, 210], [3, 140], [4, 105], [5, 84], [6, 70], [7, 60], [8, 105 / 2], [9, 140 / 3], [10, 42] |
||
|
|
||||
|
Je
connais un nombre N dont je constate qu'il est divisible par tous les nombres
de 1 à 30, à l'exception d'exactement deux nombres consécutifs. Lesquels
? On va montrer qu'il s'agit de 16 et 17: c'est donc un nombre non
divisible par 16 et 17, mais il l'est par tous les autres. |
Ce nombre est sans doute très grand S'il était divisible par tous les nombres ce serait au moins: PPCM (1 à 30) = 2 329 089 562 800 = 24 . 33 . 52 . 7 . 11 . 13 . 17 . 19
. 23 . 29 |
|||
|
Cas du nombre maximum 30 qui montre
que N est nécessairement divisible par tous les nombres de 1 à 15 |
Supposons que N ne soit pas divisible par 2, alors N n'est pas
divisible par tous les nombres pairs (2, 4, 6, 8 … 30); beaucoup trop. N est divisible par 2. … idem pour 3 à 14. Supposons que N ne soit pas divisible par 15, alors N n'est pas
divisible par 30; 2 affirmations fausses, certes, mais non consécutives. N est divisible par 15. Avec la divisibilité par 16, son multiple 32 dépasse la valeur
maximale 30. Pas de conclusion pour 16. |
|||
|
Valeur minimale de N |
N est divisible par, au moins, tous les nombres de 1 à 15, donc par le
plus petit commun multiple de ces nombres: Nmin = PPCM (1 à 30) = 360 360 = 23 . 32 . 52 . 7 . 11 |
|||
|
Tri des nombres de 16 à 30 |
Parmi les nombres de 16 à 30 certains divisent naturellement le nombre
Nmin: [16, 24], [17, 17], [18, 2 x 32],
[19, 19], [20, 22 x 5], [21, 3 x 7], [22, 2 x 11],
[23, 23], [24, 23 x 3], [25, 52], [26, 2 x 13], [27, 33],
[28, 22 x 7], [29, 29], [30, 2 x 3 x 5] |
|||
|
Conclusion |
Parmi les rescapés qui n'offre pas la divisibilité de Nmin
, seuls 16 et 17 sont deux nombres consécutifs. |
|||
|
Nombre N |
N = Nmin x 19 x 23 x 26 x 27 x 29 = 123 304 741 560 Il est bien divisible par tous les nombres de 1 à 30. Il n'est pas divisible par 16 (pas de facteur 24 dans N) et
pas par 17. |
|||
|
Valeur des quotients de N par 1 à
30 |
[1, 123304741560], [2, 61652370780], [3, 41101580520], [4, 30826185390], [5, 24660948312], [6, 20550790260], [7, 17614963080], [8, 15413092695], [9, 13700526840], [10, 12330474156], [11, 11209521960], [12, 10275395130], [13, 9484980120], [14, 8807481540], [15, 8220316104], |
[16, 15413092695/2], [17, 123304741560/17], [18, 6850263420], [19, 6489723240], [20, 6165237078], [21, 5871654360], [22, 5604760980], [23, 5361075720], [24, 5137697565], [25, 24660948312/5], [26, 4742490060], [27, 4566842280], [28, 4403740770], [29, 4251887640], [30, 4110158052] |
||
|
|
|||
|
Nous avons donné les
exemples pour k = 6 (N = 6) et pour k = 7 (N = 42). Nous avons calculé N pour k
= 10 et k = 30. Quelles sont les valeurs de
N selon k ? |
|||
|
k |
Exceptions |
N |
|
|
6 |
4, 5 |
6,
18, 42, 54, 66, 78, 102, 114, 126, 138, 162, 174, 186, 198, … |
|
|
7 |
4, 5 |
42,
126, 294, 378, 462, 546, 714, 798, 882, 966 ,… |
|
|
8 |
7, 8 |
60,
180, 300, 540, 660, 780, 900, 1 020, 1 140, 1 380, 1 500, 1 620, 1 740, 1 860,
1 980, … |
|
|
9 |
7, 8 |
180,
540, 900, 1 620, 1 980, 2 340, 2 700, 3 060, 3 420, 4 140, 4 500, 4 860, … |
|
|
10 |
7, 8 |
180,
420, 540, 900, 1 620, 1 980, 2 100, 2 340, 2 700, 2 940 … |
|
|
11 |
7, 8 |
1
980, 4 620, 5 940, 9 900, … |
|
|
12 |
7, 8 |
1
980, 4 620, 5 940, 9 900, … |
|
|
13 |
7, 8 |
25
740, 60 060, 77 220, … |
|
|
14 |
8, 9 |
60
060, 300 300, 420 420, 660 660, 780 780, … |
|
|
15 |
8, 9 |
60
060, 300 300, 420 420, 660 660, 780 780, … |
|
|
16 |
/ |
Impossible:
aucune non-divisibilité consécutive. |
|
|
17 |
16, 17 |
1 081 080, 1 801 800,
2 522 520, 3 243 240, 3 963 960, 4 684 680, 5 405 400, 6 846 840, 7 567 560,
8 288 280, 9 009 000, 9 729 720, … 1 081 080 = 360 360
x 3 1 801 800 = 360 360
x 5 |
|
|
18 |
16, 17 |
360 360 = 23 . 32 . 5 . 7 . 11 |
|
|
19 |
16, 17 |
6
846 840 = 360 360 x 19 |
|
|
20 |
16, 17 |
6
846 840 |
|
|
21 |
16, 17 |
6
846 840 |
|
|
22 |
16, 17 |
6 846 840 |
|
|
23 |
16, 17 |
157 477 320 |
|
|
24 |
16, 17 |
157 477 320 |
|
|
25 |
16, 17 |
787 386 600 |
|
|
… |
|
|
|
|
30 |
16, 17 |
123
304 741 560 |
|
Relations entre les facteurs de
ces nombres
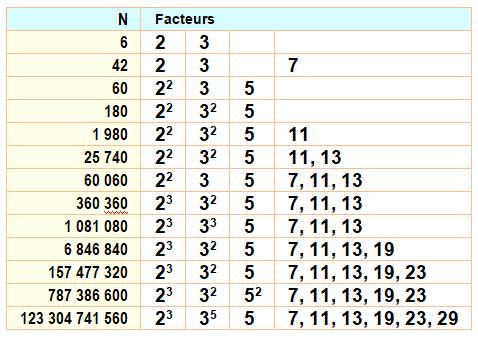
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiS2.htm
|
![]()
