|
|||||||||||||||||||||||||||
![]()
|
DIVISIBLE Une
panoplie de théorèmes indispensables. Notations: on ne sait jamais où les chercher ! Résumé
à retenir
Rappel:
le A à l'envers veut dire quel que soit;
la barre verticale équivaut à divise Également important: Lemme d'Euclide et lemme
de Gauss |
|
|
|
|
Lectures
alternatives Formulations
narratives
|
|
|
|
|
|
Exemples simples
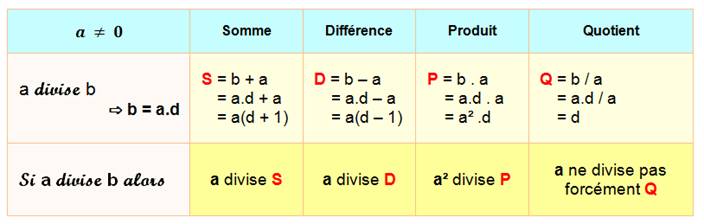
Exemples importants Si un nombre
en divise un autre, il divise leur différence. Si a
divise b, c'est que b est un multiple de a; lui
retrancher a revient à prendre le multiple juste inférieur. Ex: 13 Si un nombre en divise deux autres, il en
divise une combinaison linéaire. Si a
divise b et c, il divise u.b + v.c, u et v sont des
entiers relatifs Assez
évident en mettant en facteur avec b = a.k et c = a.h Alors: u.b
+ v.c = u.a.k + v.a.h = a (u.k + v.h) Ex: 7
divise 14 et 7 divise 35 alors 7 divise 3x14 + 10x35 = 48 + 350 = 392 = 7 x 56 Si p Ex: p = 7. Que dire de 84 = 14 x 6
? Le nombre 7 divise 14. Que dire de 98 = 14 x 7
? Le nombre 7 divise 14 et 7. Lemme de Gauss Si un nombre divise un produit et s'il est premier avec l'un des facteurs, il divise l'autre facteur. Voir Démonstration Si a Ex: a = 3 et b = 8 deux nombres sans facteur
commun (premiers entre eux ou étrangers). Que dire de 48 = 8 x 6 ? Le nombre 3 divise le facteur 6
mais pas le facteur 8. Évident! Oui en numérique mais moins sous forme
littérale et pourtant, propriété très utilisée dans les démonstrations. |
|
|
a, b, c, d, n, k, u et v sont des entiers positifs |
|
||
|
|
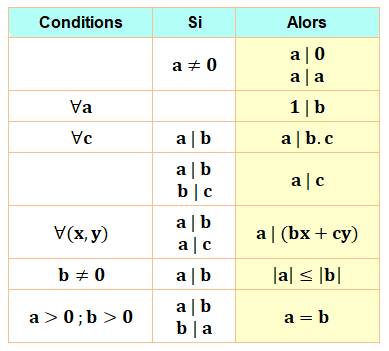
a divise a. |
||
|
|
alors a est
inférieur à b alors a
divise a + b alors a
divise a – b alors a²
divise a.b alors a2
divise b2 alors an
divise bn alors a divise k.b alors k.a
divise k.b |
||
|
|
alors a.a' divise b.b' |
||
|
|
alors a = b
au signe près. |
||
|
|
alors a divise b – c alors a divise u.b + v.c |
||
|
|
alors a
divise c Voir Démo mais, il n'est pas vrai
que a.b divise c |
||
|
|
alors p
divise a ou b. |
|
|
alors il
divise b. |
|
|
il divise au moins l'un des facteurs de ce produit. |
|
|
alors a
divise c. |
|
|
il divise b. |
|
|
il est premier avec le produit bc. |
|
|
il est premier avec b et avec c. |
|
|
toute puissance entière de a est première avec toute puissance entière de b. |
|
|
a/b et an/bm
sont des fractions minimales (non simplifiables). |
|
|
alors c
et d sont des
équimultiples de a et b respectivement: c = k.a et d = k.b |
|
|
a = |
|
|
a = 0
(tout entier a divise 0). |
|
Propriété |
Si a divise b et b
divise c |
Alors |
a divise c |
|
|
Par définition >>> |
a b |
b = c = |
a . x b . y |
|
|
À démontrer |
a |
c
= |
a . z ? |
|
|
Démonstration |
Choisissons
|
z = |
x . y |
|
|
|
Calculons
l'expression |
a . z = |
a . x . y |
|
|
|
Évaluons
cette expression |
|
(a . x) . y b . y c |
|
|
FIN |
Conclusion |
a
. z = |
c |
|
|
|
||
|
Si |
Alors |
|
|
b non nul |
|
|
|
Les
diviseurs d'un entier non nul |
sont en nombre fini. |
|
|
Tout
diviseur d d'un entier a > 0 |
|
|
|
Pour qu'un
entier a soit divisible par entier
b non nul, il faut et il suffit
que |
a / b soit un entier. |
|
Bilan
|
Nous avons vu les notions de divisibilité Le diviseur de a, s'il
existe, est un nombre compris entre 1 et a Nous sommes prêts à aborder la division Bof ! Je préfère
jouer un peu avec Divisibilité / Diviseurs |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivDivis.htm |
![]()