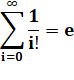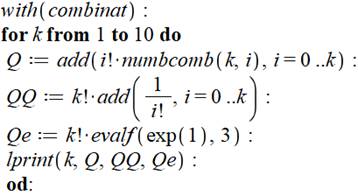|
||||||||||||||||||||||||||||||||||||||||
![]()
|
COMPTER les TRAJETS Compter les itinéraires Le problème du voyageur de
commerce consiste à minimiser son trajet pour visiter tous ses clients.
Ici, il s'agit de compter tous les trajets possibles pour rejoindre un point
d'arrivée en passant ou non par des points d'étape. |
|
|
||
|
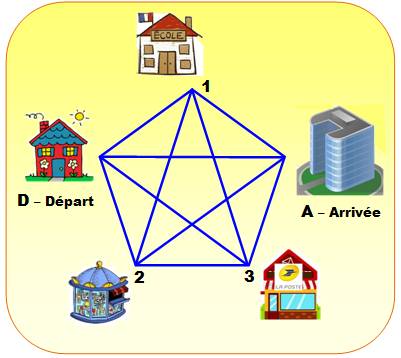
Le parcours du matin De bon
matin, Madame ou Monsieur quitte la maison pour se rendre au bureau. Selon le
jour, il faut aller déposer les enfants à l'école, chercher les journaux et éventuellement passer à la poste. Combien
de possibilités d'itinéraires se présentent à eux selon les points de passage
envisagés ? |
|
|
|
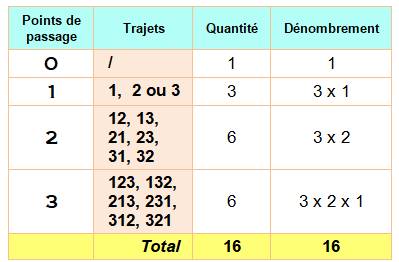
Compter les trajets possibles La
personne peut se rendre directement au bureau. Elle peut
passer par seul endroit, par deux ou trois. Le tableau montre les trajets
possibles et leur nombre selon la quantité de points de passage. Une idée pour le dénombrement: avec deux
points d'étapes, par exemple, il y a trois possibilités de choix pour le
premier, puis deux pour l'autre. |
|
|
|
|
||
|
Spécifications du problème
Maths Quantité de trajets = nombre de traits droits qu'il est possible de
tracer d'un point à un autre parmi un ensemble de k points dans le plan
cartésien en ne passant pas plus d'une fois par chaque point. |
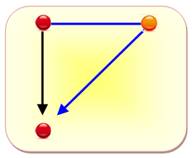
Avec un seul point de passage Deux trajets sont possibles:
Points rouges: départ et arrivée; Point orange:
point de passage. |
|
|
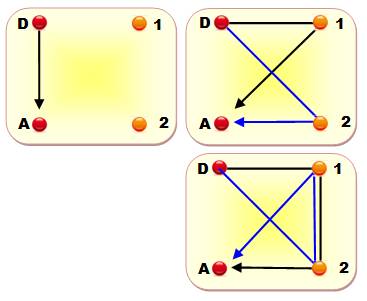
Avec deux points de passage
Un total
de 5 trajets possibles. On
constate que le trajet direct est toujours présent, de même que les k
passages par un seul point. Ce qui
veut dire que la formule de dénombrement commence par: |
|
|
|
|
||||
|
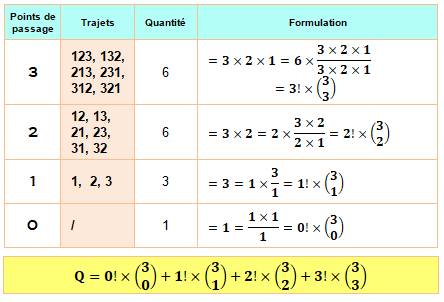
Avec trois points de passage:
|
Tableau des trajets pour trois
points de passage
Q = 1x1 + 1x3 + 2x3 + 6x1 Vous avez sans doute reconnu un problème de combinaisons:
choix de k objets parmi n, et l'introduction de leur
calcul. Vous reconnaissez aussi (en rouge), les coefficients du
binôme qui figurent dans le triangle
Pascal. |
|||
|
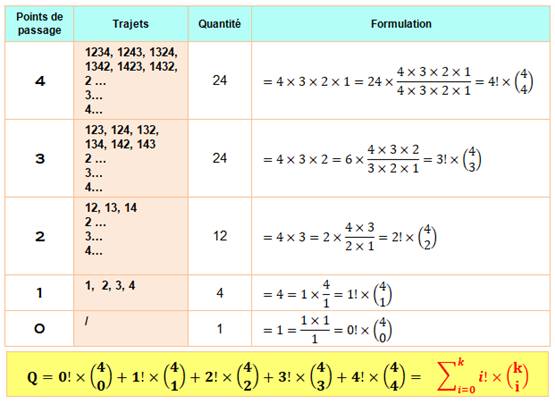
Avec Quatre points de passage: On vérifie la même logique de construction de la
formule. Et, on montre la formule générale. |
|
|||
|
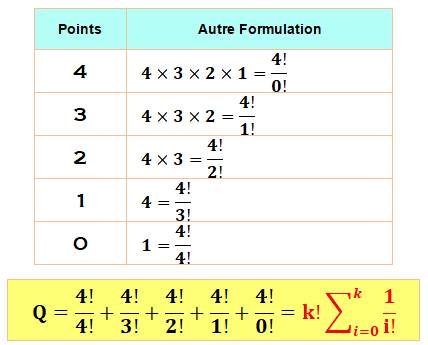
Formulation
avec factorielles uniquement Le tableau montre la mise en facteur commun de
factorielle 4 qui fait apparaître la somme des
inverses des factorielles. Or celle-ci tend vers la constante e = 2,718…
pour i tendant vers l'infini.
Soit la formule simple suivante:
|
|
|||
|
|
||
|
|
Commentaires Appel aux logiciels de combinatoire. Lancement de la boucle d'analyse des valeurs de k de 1 à 10. Calcul de Q, la somme (add) de i factorielle
multipliée par la quantité de combinaisons et pour i de 0 à k. Calcul du même type pour QQ mais avec la
formule impliquant l'inverse des factorielles. Et, troisième valeur Qe, calcul avec
l'exponentielle. En bleu les résultats. Q et QQ sont logiquement égaux. Qe n'est qu'une approximation de Q. |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()