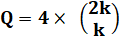carrés magiques avec des lettres

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/06/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Bases et amusements			Glossaire Carrés magiques
INDEX Carrés magiques	Latin	Gréco-latin	Avec 0 à 9
	Ésotérique	Lettres	Lettres à deviner
		Sommaire de cette page >>> Approche >>> Exemples >>> Grilles avec suite de lettres quelconques >>> Dénombrement >>> Grilles avec texte particulier >>> BONNE NOUVELLE >>> MISSISSIPPI >>> Formulation

CARRÉS MAGIQUES avec des LETTRES

MOTS CARRÉS ou MOTS en GRILLE

Deux races de mots carrés qui consistent en:

Lire des mots valides aussi bien en horizontal et en vertical; ou

Compter combien de fois le même texte est présent dans la grille.

Le plus classique de ces carrés et, sans doute, le plus ancien est: SATOR.

Non moins classique, le fameux cas de MISSISSIPPI et son orthographe extraordinaire.

Anglais: Word square / Special type of acrostic

Approche – MOTS Carrés
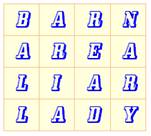
On peut lire un mot sur chaque ligne. Ces mêmes mots sont répétés en colonnes. Sur l'exemple anglais, on lit: - grange, aire, menteur et dame; - bal, aria (musique), lire et aucun.	Autres exemples: Jeu grille – Le Monde
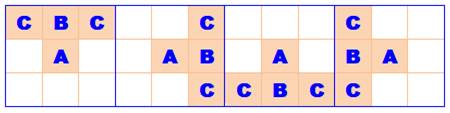
Exemples Wikipédia propose les cinq exemples suivants:

Voir Mots croisés

Grilles avec suite de lettres distinctes quelconques

Compter les mots – Énigme avec grille carrée
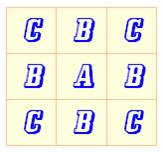
Carré 3x3 Ici, le jeu consiste à trouver combien de fois peut-on écrire ABC en suivant un chemin par pas successifs horizontaux ou verticaux. Avec une grille 3x3, la réponse est assez simple: 4 fois 2 chemins = 8 possibilités. En effet, depuis le point A: 4 possibilités et arrivé en B, deux choix possibles: 4 x 2 = 8.	4 x 2 = 8
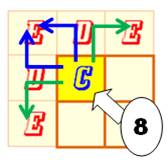
Carré 5X5 Une couronne de lettres D et E à été ajoutée. Comme nous venons de le voir, il y a 8 chemins pour atteindre les C de la grille centrale 3x3. Pour chacun (Voir illustration – détail), il y a 2 possibilités pour faire DE et atteindre un sommet (bleu); et il y a également 2 possibilités pour atteindre le E du milieu (vert). Bilan 8 fois (2 sommets + 2 milieux) = 32 possibilités		Détail de comptage 8 x 4 = 32
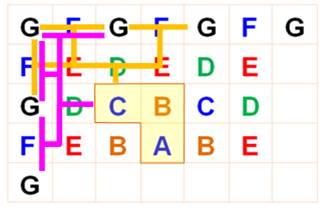
Carré 7x7 Une couronne de lettres F et G à été ajoutée. On atteint le E sommet par 8x2 = 16 chemins avec 2 possibilités pour aller jusqu'à un G sommet et 2 possibilités pour aller à un G milieu, soit 64 possibilités. On atteint le E milieu par 8x2 = 16 chemins avec 2 possibilités pour aller jusqu'à G, soit 32 possibilités. Bilan 32 + 32 + 32 = 96 chemins possibles en partant de A pour arriver à G Vérification Le schéma ci-contre montre comment compter les chemins à partir de C, sachant qu'il y a 8 possibilités pour arriver à un des quatre C. Alors 2 x 6 routes se dessinent: les 6 en ocre et les 6 en rose. On retrouve notre bilan: 8 x 12 = 96. On note les quatre arrivées au sommet par les 8 chemins pour C, soit 32 manières d'arriver au sommet et, par différence: 64 chemins pour arriver aux G des côtés.		Détail de comptage À partir de C, il y a 2 x 6 routes pour arriver à G.

Voir Approche de ce problème par celle du dénombrement des chemins dans une grille (Triangle de Pascal)

Dénombrement

Sommets = 2 fois la quantité de la ligne précédente.

Milieux atteints comme pour les sommets et en plus 2 fois la quantité pour les milieux précédents.

On retrouve bien les 8, 32 et 96 analysés ci-dessus.

Rang	Grille	Sommets	Milieux	Total
1	1 x 1	1
2	3x3	4 x 2		8
3	5x5	8 x 2	8 x 2	32
4	7x7	16 x 2	16 x 2 16 x 2	96
5	9x9	32 x 2	32 x 2 64 x 2	256
6	11 x 11	64 x 2	64 x 2 192 x 2	640
7	13 x 13	128 x 2	128 x 2 512 x 2	1 536
8	15 x 15	256 x2	256 x 2 1 280 x 2	3 584

Formule de récurrence

S₂ = 8; M₂ = 0
S_n = 2S_{n- 1} ; M_n = 2S_{n- 1} + 2M_n-1 ; T_n = S_n + M_n

Formule

Polynôme générateur

Valeurs

1, 8, 32, 96, 256, 640, 1 536, 3 584, 8 192, 18 432, 40 960, 90 112, 196 608, 425 984, 917 504, 1 966 080, 4 194 304, 8 912 896, 18 874 368, 39 845 888, 83 886 080 …

Grilles avec texte particulier

Approche

Sur la grille 3x3, on peut lire le mot ÉTÉ huit fois à partir du centre et quatre fois 4 fois à partir des sommets.
Total: 8 + 4 x 4 = 24 façons de lire de mot ÉTÉ.

Sur la grille 5x5, on peut lire le mot MESSE à partir du M du centre.
En partant vers le haut et en bifurquant à gauche, il y a trois façons de lire MESSE.
Il y a huit manières de partir du M central.
Total: 8 x 3 = 24 façons de lire de mot MESSE.

Je ne vois pas bien la manière de décompter. Alors, laissez-vous guider avec l'exemple suivant.

BONNE NOUVELLE – Grille 13x13

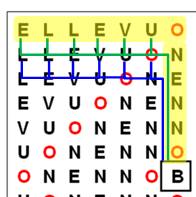
Ce jeu d'itinéraire, du même type que ceux précédents, m'a été proposé par Jérôme Meyer. Il s'agit d'une grille 13x13.

Énigme

Sur cette grille combien de fois peut-on lire BONNE NOUVELLE (sans espace) en progressant horizontalement et verticalement sur la grille ?

Tous les sens sont autorisés, mais chaque lettre n'est utilisée qu'une seule fois. Exemple montré en jaune.

Premières observations

Le départ de l'itinéraire en B central est unique.

Le O voisin du B est celui de BONNE et, celui du grand carré rouge oblique est pour le O de NOUVELLE.

Les L de NOUVELLE se trouvent au-delà du carré rouge de O. L'itinéraire se termine donc dans cette zone des coins et, le E final est celui des sommets.

Conclusion: tous les chemins partent du B central et finissent au E des sommets. De plus, la progression vers le sommet est continue. Par exemple, vers le haut et à gauche pour le sommet en haut à gauche.

En jaune, un chemin qui montre la construction des itinéraires à partir du B central.

Tous ces chemins partent du B central et finissent aux sommets E en circulant le long d'une sorte de diagonale brisée.

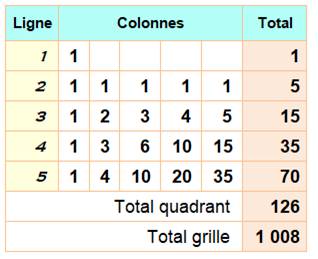
Le périmètre

Avec les médianes et les côtés, il est possible d'écrire 8 fois BONNE NOUVELLE.

Du fait des symétries, l'analyse d'un quadrant suffit. Les résultats seront à multiplier par 8.

On sélectionne le quadrant haut-gauche jaune. C’est-à-dire les mots qui commencent par BO et se poursuivent vers le haut et vers la gauche.

Figure symétrie avec 2 x 4 motifs

La deuxième ligne

On forme BONNEN en vertical, et la suite en horizontal peut être obtenue en bifurquant n'importe où vers la ligne du haut (traits verts).

Soit 6 chemins pour écrire notre texte.

Total: 6 + 1 chemins pour les deux premières lignes de ce quadrant.

Chaque chemin de la 2^e ligne peut profiter de la première ligne.

La troisième ligne

On forme BONNE en vertical, et la suite en horizontal peut être obtenue en bifurquant n'importe où vers la ligne du haut ET en prenant n'importe quel chemin des chemins de la deuxième ligne:

Avec BONNEN et O, il y a 6 chemins;

Avec BONNENO et U, il y a 5 chemins;

…

Avec BONNENOUVEL, il a un seul chemin.

Bilan: 6 + 5 + 4 + 3 + 2 + 1 = ½ 6x7 = 21 chemins

Chaque chemin de la 3^e ligne profite de tous les chemins possibles en haut et à gauche.

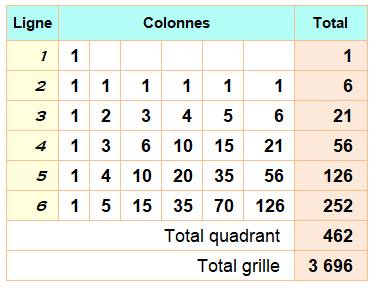
Lignes suivantes

Même principe: chaque ligne profite des chemins du dessus à gauche.

Par exemple, en ligne 4, après la montée verticale la première bifurcation vers la gauche profite des 21 + 15 + 10 + 6 + 3 + 1 = 56 chemins du dessus.

Bilan: la grille comporte 8 x 462 = 3 696 fois le texte BONNE NOUVELLE.

Voir Nombres triangles (ligne 3), tétraédriques (ligne 4), Pentatopes (ligne 5)

MISSISSIPPI – Grille 11x11

Le nom de cet état des États-Unis se prête à de nombreux jeux comme celui des mots carrés.

Voir États-Unis

Voir Anagrammes de Mississippi

Combien de fois peut-on lire le mot MISSISSIPPI dans cette grille ?

Le même type de calcul que précédemment montre que le nom MISSISSIPPI est écrit 1 008 fois dans la grille.

Formulation

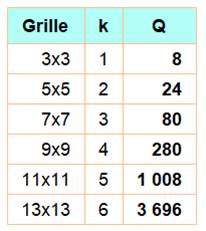
Formule

Valeurs de Q

8, 24, 80, 280, 1008, 3696, 13728, 51480, 194480, 739024, 2821728, 10816624, 41602400, 160466400, 620470080, 2404321560, 9334424880, 36300541200, 141381055200, 551386115280, 2153031497760, 8416395854880, 32933722910400, 128990414732400, 505642425751008, 1983674131792416, 7787757702592448, 30594762403041760, 120269065998164160, 473058326259445696

Voir Triangle de Pascal – Table des valeurs

Voir Combinaisons

Quantité de lectures d'un mot

Exemple: écrit dans une grille 7x7, un mot de sept lettres, comme MIMOSAS, peut être lu 80 fois dans la grille.

Suite	Carrés magiques d'ordre 6 Carrés magiques - devinettes Carrés magiques à contraintes Carrés magiques – Jeux Carrés magiques triples de Pythagore
Voir	Carrés magiques – Index Cryptarithme Lettres de l'alphabet Mots croisés
DicoNombre	Nombre 8 Nombre 32 Nombre 1 008 Nombre 3 696
Sites	Carré magique (lettres) – Wikipédia OEIS A241204 – Expansion of (1 + 2x)^2/(1 - 2x)^2. OEIS A146534 – 4C(2n,n)-30^n
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMLettre.htm