le petit théorème de Fermat et n puissance k moins n

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/10/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Général	Le petit théorème de Fermat			Glossaire Général
INDEX Théorie des nombres	Découverte	Exploration	Démonstration	Généralisation
	Perles et collier	Applications	Puissances	Avec Pascal
		Sommaire de cette page >>> Exemples de divisibilités >>> Divisibilité de n^p – n Analyse détaillée >>> n² – n >>> n³ – n >>> n⁵ – n >>> Analyse pour p suivants: de 7 à 17 >>> Bilan de divisibilité pour p de 2 à 53

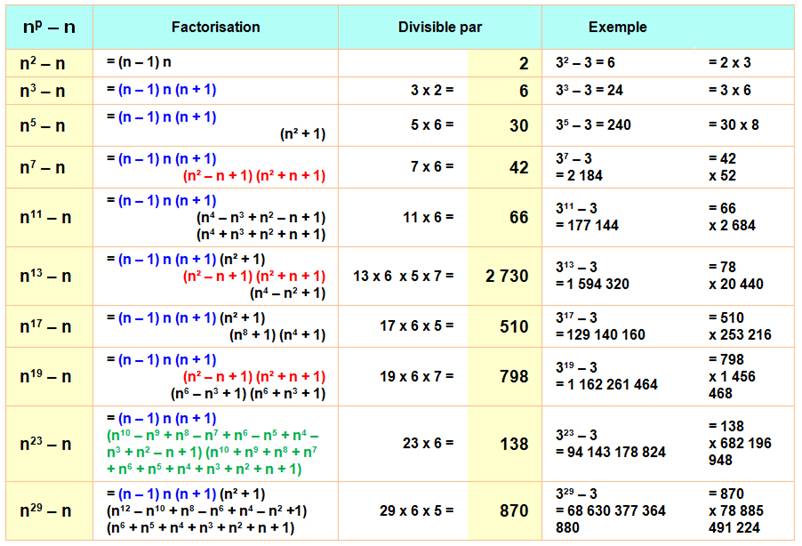
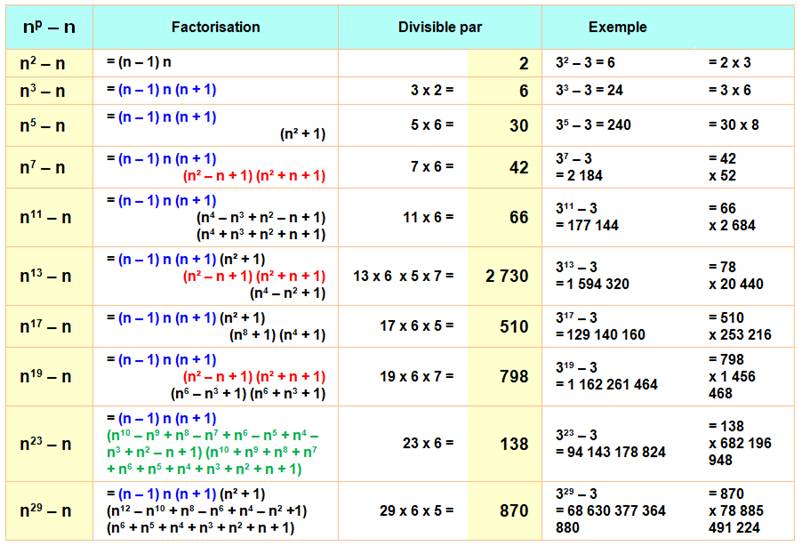
PETIT THÉORÈME DE FERMAT

Applications directes à n^p – n

Déductions immédiates du petit théorème de Fermat sur la forme cette forme polynomiale simple.

Exemple: n¹³ – n est divisible 2 730

Exemples de divisibilité de n^p – n

Divisibilité de n^p – n

haut

Liste des facteurs de divisibilité de

n^p – n

Étonnamment, les diviseurs communs de n^p – n se révèlent être les mêmes que les dénominateurs des nombres de Bernoulli. Ces derniers apparaissant de façon récurrente dans les problèmes de dénombrement, dans les formules de sommes de puissances entières, et jusque dans le développement en série de fonctions analytiques fondamentales. 

(2, 2), (3, 6), (5, 30), (7, 42), (11, 66), (13, 2730), (17, 510), (19, 798), (23, 138), (29, 870), (31, 14322), (37, 1919190), (41, 13530), (43, 1806), (47, 282), (53, 1590), (59, 354), (61, 56786730), (67, 64722), (71, 4686), (73, 140100870), (79, 3318), (83, 498), (89, 61410), (97, 4501770), (101, 33330), (103, 4326), (107, 642), (109, 209191710), (113, 1671270), (127, 4357878), (131, 8646), (137, 4110), (139, 274386), (149, 4470), (151, 2162622), (157, 1794590070), (163, 130074), (167, 1002), (173, 5190), (179, 1074), (181, 7225713885390), (191, 12606), (193, 868841610), (197, 171390), (199, 244713882), (211, 9225988926), (223, 9366), (227, 1362), (229, 625170), (233, 412410), (239, 1434), …

OEIS A166062 - a(n) = denominator(Bernoulli(prime(n) - 1)).

Programme Python: divisibilité

import math

from sympy import primerange

def pgcd_liste(vals):

g = 0

for v in vals:

g = math.gcd(g, v)

return g

def doublets_premiers_pgcd():

doublets = []

for p in primerange(2, 240):

npn = [n**p - n for n in range(2, 21)]

g = pgcd_liste(npn)

doublets.append((p, g))

return doublets

if __name__ == "__main__":

print(doublets_premiers_pgcd())

But

Lister les doublets (premier, diviseur) caractérisant la divisibilité de n^p – n.

Commentaires

pgcd_list calcule le PGCD (gcd en anglais) d'une liste de nombres.

Pour le calcul des doublets, deux boucles:
l'une balaie les nombres premiers et, pour chacun, l'autre calcule la valeur de n^p – n pour n de 2 à 20 (exemple).

Calcul du PGCD de tous ces résultats pour chaque p et formation des doublets.

Programme principal (main) qui affiche les doublets.

Résultats

Voir la liste ci-dessus.

Programme Python: Bernoulli

from sympy import bernoulli, isprime

def denom_bernoulli(n):

b = bernoulli(n)

num, den = b.as_numer_denom()

return int(den)

for k in range (1,20):

if isprime(k):

dbern = denom_bernoulli(k-1)

print(k,dbern)

But

Calculer le dénominateur des nombres de Bernoulli pour p – 1.

Commentaires

Python/Sympy contient la fonction de calcul de ces nombres.

Résultats

2 2

3 6

5 30

7 42

11 66

13 2730

17 510

19 798

Voir Programmation – Index / Programmes Python – Index

Analyse détaillée

n² – n divisible par 2
L'exposant 2 est un nombre premier. Application du PTF. Les trois formulations sont équivalentes.	n² – n = 2 k Ce qui veut dire que ce polynôme est divisible par 2; il est toujours pair. Ex: 3² - 3 = 9 – 3 = 6
Nous avons une confirmation directe sans le PTF. En effet, factorisons:	n² – n = (n – 1) n Succession de deux nombres, dont l'un est forcément pair et le produit est pair.

n³ – n divisible par 6

PTF direct avec 3

L'exposant 3 est un nombre premier.
Application du PTF:

Ce qui veut dire que ce polynôme est divisible par 3.

Ex: 3³ - 3 = 27 – 3 = 24

Factorisation

Elle nous montre que ce polynôme est divisible par 6.

n³ – n = (n – 1) n (n + 1)

Succession de trois nombres.

L'un d'eux au moins est pair, et

L'un d'eux au moins est divisible par 3.

n³ – n = 6 k

PTF supplémentaire avec 2

Cette indication nous incite à revoir le PTF sur ce polynôme de la manière suivant.

On montre que ce polynôme est aussi divisible par 2.

Divisible par 3 et par 2, il l'est par 6.

En mod 2:

Derrière le signe de congruence, n² est équivalant à n.

Récurrence

La divisibilité par 6 se démontre également facilement par récurrence.

Initialisation

n³ – n est divisible par 6 pour n = 0.

Calcul d'hérédité

Supposons la vraie pour k_n

n³ – n = 6k

Et calculons sont expression pour n +1

E_n+1 = (n + 1)³ – (n + 1) = n³ + 3n² + 3n + 1 – n – 1

= n³ – n + 3n(n + 1) = 6k + 3n(n + 1)

Or n et (n + 1) sont deux nombres consécutifs; l'un d'eux est pair est n (n + 1) est divisible par 2.

E_n+1 = 6k + 3 x 2h = 6 (k + h), divisible par 6.

Conclusion

Si la divisibilité par 6 est vraie pour n, alors elle est vraie pour n + 1, or elle est vraie pour 0; elle est toujours vraie.

Trois méthodes

Nous venons de voir trois méthodes pour démontre que n³ – n est divisible par 6:

par factorisation et constat de trois nombres consécutifs

par récurrence, et

par l'emploi du petit théorème de Fermat à répétition (pour p = 2 et pour p = 3).

n⁵ – n divisible par 30

Nous allons utiliser le PTF en cascade avec les nombres premiers successifs inférieurs à 5, soit ici: 2 et 3.

Les deux colonnes de gauche indiquent la propriété de base déduite du PTF.
La colonne centrale en blanc montre le calcul du modulo de la puissance concernée, ici 5.

Exemple de lecture: en modulo 3, le PTF nous dit que n³ – n est divisible par 3. En partant de n⁵ nous cherchons à sortir autant de cubes que possible, ici un seul. Chaque cube est remplacé par n en modulo 3 conformément à notre PTF. Au final n⁵est identique à n en modulo 3. Ils sont même reste lorsque divisés par 3. Leur différence n³ – n est divisible par 3.