|
|||||||||||||||||||||||||||||||||||||||||||||
On dit primarité (français) ou primalité
(avec teinture anglo-saxonne)
![]()
|
LES PRESQUE NOMBRES PREMIERS & PSEUDO-PREMIERS 1) Par leurs facteurs:
Les presque-premiers ou k-presque-premiers
comprennent exactement k facteurs
premiers. 2) Par leur résistance
aux tests de primalité: ce sont les pseudo-premiers.
Déterminer
si un nombre est premier, ce
n'est pas si simple ! On va découvrir des nombres pseudo-premiers, les nombres de
Poulet et d'autres encore "plus presque" premiers, les
pseudo-premiers absolus de Carmichael. L'existence
de ces nombres singuliers créé une difficulté pour la recherche de la primalité des
nombres: pas de critères absolus pour déterminer si un nombre est premier ou composé. |
|
|
||
|
Définition Un entier n > 0 est dit
k-presque premier, pour k |
Exemples
Voir Tables |
|
![]()
Les pseudo-premiers
|
|
|||
|
Petit théorème de
Fermat – Version faible
|
Lecture Quand p est
premier, un nombre a et sa
puissance p ont même
reste lorsque divisés par p. Ex: 75
= 16 807 = 5 x 3 361 + 2 et 7 = 5 x 1 + 2 Ce qui donne: 75 – 7 = 5 x 3 360 + 0 |
||
|
Petit théorème de
Fermat – Version forte En divisant par a, avec précaution
Voir Petit théorème de Fermat -
Développements |
Lecture Avec p est premier
et a non multiple de p, le nombre a et sa
puissance p ont même
reste lorsque divisés par p. Ex: 75-1
– 1 = 2 400 = 5 x 480 + 0 Sans calculer, que dire
de 7100 divisé par le nombre premier 101. Ce nombre n'est pas
multiple de 100, alors:
Le reste est égal à 1. |
||
|
Réciproque fausse Magnifique théorème qui marche dans un sens, mais pas toujours
dans l'autre: ce n'est pas parce que p est composé que cette expression n'est
plus divisible par p. |
Il existe des nombres
composés qui satisfont le petit théorème de Fermat (sorte de filtre)
|
|
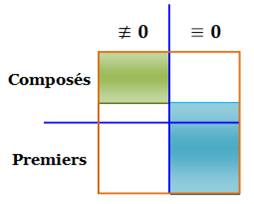
Test avec tous les
nombres Si on
teste cette divisibilité pour tous les nombres:
La seule
chose sure, c'est que le test n'élimine que des nombres composés (vert). Si le test
montre la divisibilité, on a probablement un nombre premier, mais ce n'est
pas sûr (bleu). |
Schéma qui résume la
situation
|
|
|
|||
|
Test de Fermat –
Version forte
|
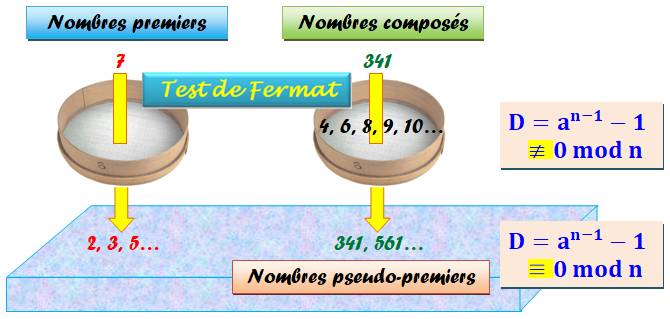
Le test de Fermat n'élimine que des
nombres composés. C'est sûr ! Si on sait a priori que n est
premier, alors c'est certain, il passe le test. Mais, dans notre cas, nous ne
savons pas si n est composé ou premier. Alors ? Malheureusement, certains nombres
dissipés passent le test tout en étant composés. Ce sont des trouble-fêtes,
appelés pseudo-premiers Les pseudo-premiers
sont des nombres composés qui divisent D sans être premiers. |
||
|
Visualisons un peu ces
choses!
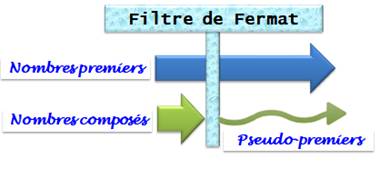
Tous les
nombres premiers passent bien à travers le tamis ou le filtre (test de
Fermat). Hélas
quelques nombres composés aussi: les pseudo-premiers |
|||
Généralisation
|
Il existe d'autres filtres
que celui basé sur le petit théorème de Fermat, comme la condition d'Euler.
Tous ces nombres composés qui passent malgré tout à travers le filtre sont
des nombres pseudo-premiers. Tous ceux qui
passent le filtre, y compris les nombres premiers, sont des probablement premiers. Avec la condition de Fermat et
selon la base a
utilisée, on dit. Sans confusion possible, la mention Fermat est omise pseudo-premiers de
base a, parfois abrégé en a-PP. |
|
|
||
|
On va les dévoiler
tout de suite: il existe des pseudo-premiers encore plus coriaces: les pseudo-premiers absolus. |
Si on avait eu l'idée de se dire: OK! Le
test de Fermat ne marche pas pour une valeur de a, mais en effectuant le test pour plusieurs valeurs
de a et par recoupements, on devrait y arriver. C'est loupé! Car il existe des nombres
rebelles pour lesquels la divisibilité est possible pour toutes les valeurs
de a: les pseudo-premiers absolus et les nombres de
Carmichael. |
|
|
|
|
|
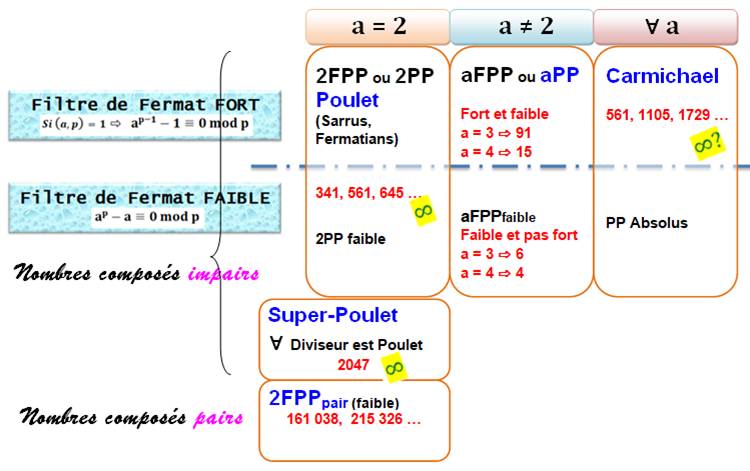
Deux critères pour
classer les nombres pseudo-premiers de Fermat (FPP): La valeur de la base a & le type de condition de Fermat, forte ou
faible
|
|
Explications du tableau de synthèse
|
a = 2 |
Nombres
de Poulet ou Pseudo-premier de Fermat à
base 2 (2FPP). Ne concernent que les nombres impairs ! Si p est un premier impair, il est toujours premier
avec a. Alors, les nombres de Poulet (condition faible) sont aussi nombres
pseudo-premiers en base a. Le premier fut découvert par Sarrus, d'où le nom
alternatif. On parle aussi de Fermatians (peu utilisé). Il y en a une infinité dont une infinité de Mersenne. Dans le cas où, en plus tous les diviseurs de n
sont des nombres de Poulet, on le nomme nombre super-Poulet.
Il y en a une infinité. On ne sait pas s'il y en a une infinité de Mersenne. Il existe des pseudo-premiers pairs à base 2 qui
passent le test faible et pas le fort.
Ce sont les nombres pseudo-premiers pairs
de Fermat à base 2 (2Fpppair). En anglais: even 2FPP. Il n'existe pas de super-Poulet pairs. |
|
a |
Certains nombres
composés passent le test de Fermat pour certaines valeurs de a autre que 2.
Certains pour le test faible uniquement. Ce sont les pseudo-premiers
faibles à base a (aPPfaible). D'autres passent à travers
les deux conditions, les pseudo-premiers forts à
base a (aPP). |
|
|
Les
pseudo-premiers qui passent le test faible pout routes les valeurs de a sont
des pseudo-premiers absolus (PPA). Avec le test fort ce sont les nombres de
Carmichael (trouvé par lui en 1909). On montre que tout PPA est Carmichael et
réciproquement. On ne sait pas s'il y en a une infinité. |
Référence pour ces
explications: le
livre de Sierpinski
|
|
|
|
Avec la base a = 2, le test de Fermat se trompe dans
seulement 1 cas sur un million. Les pseudo-premiers sont rares ! Et encore plus rares
pour a plus grand. Le test de Fermat avec la base 2 détecte des nombres
composés dans 95,64 % des cas et des nombres probablement premiers dans 4, 36
% des cas, dont 0,00009% sont des pseudo-premiers (nombres de Poulet). |
|
Source: Merveilleux
nombres premiers page 266
|
|
|||||
|
|
||||
|
Pseudoprimes
to base 3 |
Composite numbers
n such that 3^(n-1) == 1 (mod n). Such
as 91, 121, 286, 671, 703, 949, 1105, … |
||||
|
Carmichael
numbers |
|
||||
Voir
Anglais pour le
bac et pour les affaires
Merci à Stephan
CEROI pour les précisons importantes
apportées à cette page
![]()
Suivre le lien pour plus
de précisions sur ces types de nombres
Un nombre typique permet d'accéder au dictionnaire des
nombres
|
Suite |
|
|
Voir |
|
|
|
|
|
Sites |
|
|
Cette page |
![]()