NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/03/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Théorie des Nombres
Débutants Général	Le petit théorème de Fermat				Glossaire Général
INDEX Théorie des nombres	Découverte	Exploration	Démonstration		Généralisation
		Applications	Puissances		Avec Pascal
		Sommaire de cette page >>> Tableau récapitulatif >>> Carrés >>> Cubes >>> Bicarrés		>>> Puissance 5 >>> Puissance 6 >>> Puissance 7 >>> Puissance 10 >>> Puissance 11

PETIT THÉORÈME DE FERMAT

& Puissances des nombres

Déductions immédiates du Petit Théorème de Fermat (PTF) sur la forme de la puissance des nombres.

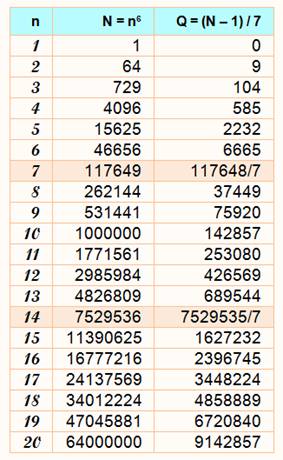
Voir PTF et le polynôme n^k – n

Carrés
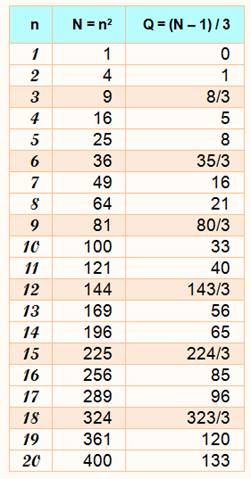
Petit théorème de Fermat avec p = 3 a^3 - 1– 1 = 0 mod 3 2^2 – 1 = 0 mod 3 3^2 – 1 0 mod 3 4^2 – 1 = 0 mod 3 5^2 – 1 = 0 mod 3 6^2 – 1 0 mod 3 Tous les carrés sont de la forme 3k + 1, sauf pour les nombres divisibles par 3.

Cubes
Petit théorème de Fermat avec p = 3 a^3– a = 0 mod 3 2^3 – 2 = 0 mod 3 3^3 – 3 = 0 mod 3 4^3 – 4 = 0 mod 3 5^3 – 5 = 0 mod 3 6^3 – 6 = 0 mod 3 Tous les cubes sont de la forme: n^3 = 3k + n

Bicarrés (P4)
Petit théorème de Fermat avec p = 5 a^5 - 1– 1 = 0 mod 5 Tous les bicarrés sont de la forme 5k + 1, sauf pour les nombres divisibles par 5.

Puissance 5
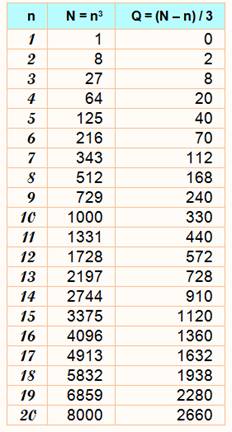
Petit théorème de Fermat avec p = 5 a^5– a = 0 mod 5 Toutes les puissances 5 sont de la forme 5k + n.

Puissance 6
Petit théorème de Fermat avec p = 7 a^7 - 1– 1 = 0 mod 7 Toutes les puissances 6 sont de la forme 7k + 1, sauf pour les nombres divisibles par 7.

Puissance 7
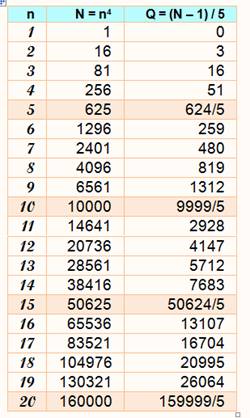
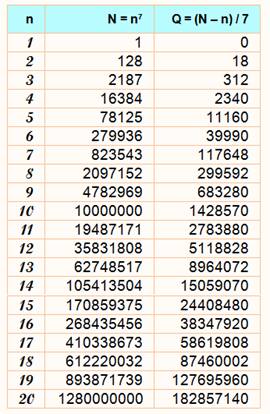
Petit théorème de Fermat avec p = 7 a^7– a = 0 mod 7 Toutes les puissances 7 sont de la forme 7k + n.

Puissance 10
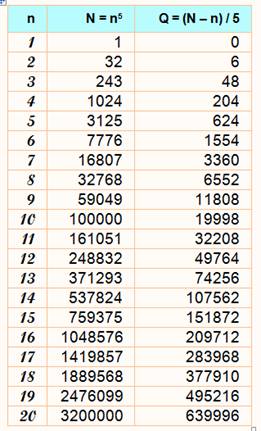
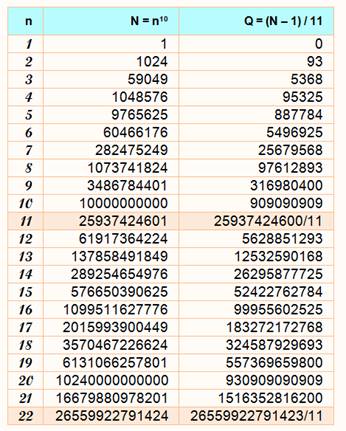
Petit théorème de Fermat avec p = 11 a^11 - 1– 1 = 0 mod 11 Ex: 4^10 / 11 a un reste égal à 1. En effet: 4^10 = 1 048 576 = 95 325 x 11 + 1 Toutes les puissances 10 sont de la forme 11k + 1, sauf pour les nombres divisibles par 11.

Puissance 11
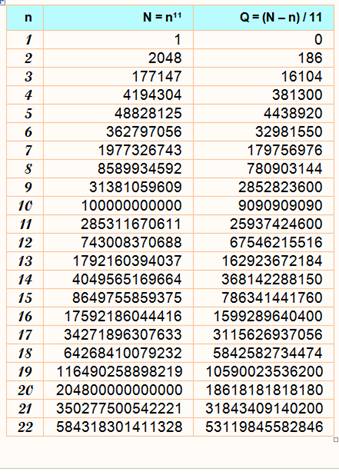
Petit théorème de Fermat avec p = 11 a^11– a = 0 mod 11 Ex: 4^11 / 11 a un reste égal à 4. En effet: 4^11 = 4 194 304 = 381 300 x 11 + 4 Toutes les puissances 11 sont de la forme 11k + n, sauf pour les nombres divisibles par 5.

Tableau
Premier	Forme de la puissance	Conditions	Exemples
p = 3	n^2 = 3k + 1 n^3 = 3k + n	sauf si 3 n n	4^2 / 3 reste 1 3^3 / 3 reste 3 soit 0
p = 5	n^4 = 5k + 1 n^5 = 5k + n	sauf si 5 n n	4^4 / 5 reste 1 3^5 / 5 reste 3
p = 7	n^6 = 7k + 1 n^7 = 7k + n	sauf si 7 n n	4^6 / 7 reste 1 3^7 / 7 reste 3
p = 11	n^10 = 11k + 1 n^11 = 11k + n	sauf si 11 n n	4^10 / 11 reste 1 3^11 / 11 reste 3
p = 13	n^12 = 13k + 1 n^13 = 13k + n	sauf si 13 n n	4^12 / 13 reste 1 3^13 / 13 reste 3
etc.
Exemple de déduction {3^3, 3^5 , 3^7, 3^11, 3^13, … 3^p, …} divisés par leur exposant donne 3 pour reste.

Suite	Le petit théorème de Fermat Découverte Exploration
Voir	Nombre pseudo-premier Test de primalité Divisibilité par 11 Divisibilité par 42
Cette page	http://villemin.gerard.free.fr/ThNbDemo/PtThFePu.htm