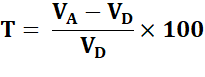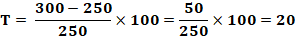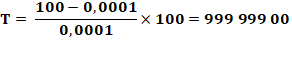|
|
Variation Aujourd'hui,
je pèse 80 kg
alors que l'an dernier à la même époque ma balance indiquait 70 kg. C'est
une différence de poids de 80 – 70 = 10 kg en un an. C'est
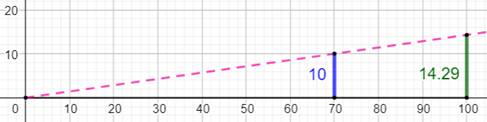
une variation de 10 kg ou encore une croissance de 10 kg. Pourcentage Avec
70 kg comme référence, mon poids a augmenté de 10 kg. Pour
mon ami qui pesait 100 kg, quel serait son poids aujourd'hui s'il avait
augmenté dans les mêmes proportions ? Le
dessin montre que son poids serait de 100 + 14,29 = 114,29 kg
On
dit que le taux de variation (ici, un taux
de croissance) est de 14,29 |
Voir Théorème
de Thalès
![]()
|
|
Taux
de variation:
qualifie l’évolution relative entre deux valeurs sur une période donnée.
C'est la variation de la grandeur par rapport à sa valeur d'origine.
Le
taux de variation s'exprime par un pourcentage. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Usage |
Notion
principalement utilisée en statistiques.
À
ne pas confondre avec le coefficient de variation: le coefficient de variation (CV) est
le rapport de l'écart-type à la moyenne.
Plus la valeur du coefficient de variation est élevée, plus la dispersion
autour de la moyenne est grande. Il est généralement exprimé en pourcentage. Dans le domaine des
mesures, on parle de précision relative. Ex: L =
110 m à 10% près. Alors, la précision est de 11 m en plus ou en moins.
Alors: 99 m < L < 121 m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calcul |
Données
Formule de calcul
Exemple Charges
locatives passant de 250 à 300 euros par mois:
On
dit alors que le taux de variation est de 20 pourcent (20%). Note Le
PIB de ce pays
était de 5% en 2000 et 8% en 2001. On dit qu'il a connu une augmentation de 3
points. On ne calcule par un taux de variation sur ces deux taux de
variation. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemples Mesures
positives |
Taux de variation positif (croissance)
Taux de variation négatif (décroissance)
|
![]()
|
Valeurs négatives |
Passer de -10 à -5
est (par exemple):
Division
par la valeur absolue de VD.
Division
par la valeur signée de VD. Illustration
|
||||||||||||||||||||
|
Valeur nulle |
MÉGA précaution ! Le diviseur ne doit
jamais être nul pour éviter la division
par 0. Exemple Cette voiture passe
de l'arrêt à 100 km/h en 10 secondes
Parler
du taux de variation dans ce cas n'a pas de sens. Tout
au plus, on pourrait dire qu'il très grand, voire infini … En
effet, si au lieu d'être immobile, la voiture roulait à 0,0001 km/h au
départ, on aurait une très grande valeur:
|
||||||||||||||||||||
|
Cas de la
température Pas bon ménage avec le zéro |
Dans
la majorité des cas, avec nos unités,
le zéro est l'origine des mesures (0
mètre, 0 kilogramme, 0 km/h, 0 euro,
etc.) et le taux de variation se calcule pour des valeurs non nulles. Le cas
nul n'a pas de sens. En
revanche, il existe des grandeurs dont le zéro
est fixé par convention. C'est le cas de la température exprimée en
degrés Celsius.
On
évitera donc de parler de taux de variation avec cette unité de température,
sauf à:
Moralité: avec les
températures mieux vaut parler d'écart de température. NB. La
phrase "En une semaine, on est
passé de 15°C à 30°C, alors il fait deux fois plus chaud" n'a aucun
sens. Voir la
vidéo citée en référence. |
||||||||||||||||||||
|
Bilan |
1.
Le taux de variation s'applique généralement à des
mesures dont les valeurs sont positives non nulles, et la formule s'applique
normalement. 2.
En présence de valeurs négatives au départ, on divisera
par cette valeur ou sa valeur absolue selon le sens que l'on veut donner à la
variation. 3.
Le cas d'une valeur de départ nulle n'a pas de sens,
sauf à assimiler le résultat à l'infini. |
![]()
|
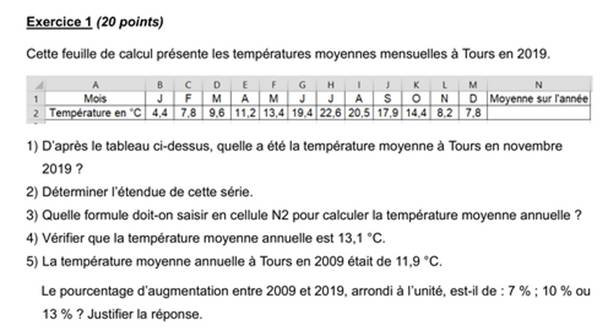
Brevet 2021 Sujet qui fait intervenir le
taux de variation des températures. VOIR les remarques à propos
des températures, vues ci-dessus Voir Brevet |
Corrigé 1) En novembre 2019, la température moyenne
était de 8,2 °C (par lecture dans le tableau). 2) Température la plus basse: 4,4 °C 3) Formule de calcul de la moyenne: 4) Calcul de la moyenne (4,4 + 7, 8, + …+ 7,8)
/ 12 = 13,1 °C 5) Taux de variation; ici taux d'augmentation: Valeur
d'arrivée: 13,11 °C Le
taux de variation (arrondi) est 10% |
Merci
à Jean-Marc Levesque
pour ses remarques à propos de la température
|
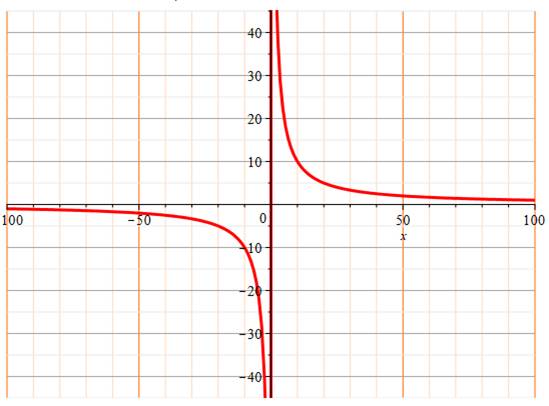
Interprétation Graphe qui montre avec quelle
prudence il faut interpréter un taux de variation |
Le
taux de variation donne une proportion de
variation d'une grandeur par rapport à une valeur
de référence, le point de départ. Pour
un même écart, plus la valeur de départ est petite et plus le taux de variation est grand. En
s'approchant d'une valeur nulle, le taux tend vers l'infini. Ce
graphe montre l'allure en hyperbole
de la variation du taux en conservant un écart constant.
Lecture du graphe:
la courbe est construite pour un écart unité. Avec une valeur de départ de 10, le taux est
10%; avec 50 on aura 2%. |
|
Aussi |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()