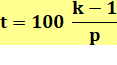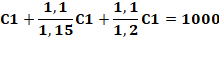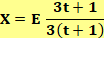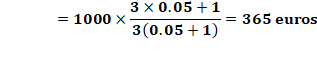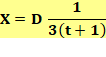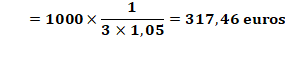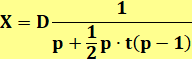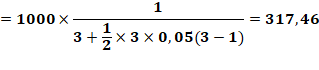NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/09/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Économie
Débutants Fractions	INTÉRÊTS			Glossaire Pourcentages
INDEX Calcul Économie	Intérêts simples	Intérêts composés	Rente	Comparaisons
		Intérêts – Calculs
		Sommaire de cette page >>> Intérêts simples >>> Exemples >>> Exercices >>> Emprunts >>> Anglais

Calculs d'intérêts

Je place mon argent. Combien me rapporte-t-il?

Deux cas:

Intérêts simple: même rapport chaque année (ou autre période)

Intérêts composés: production d'intérêts également sur les intérêts déjà acquis.

Cette page est consacrée aux intérêts simples.

Intérêts Simples

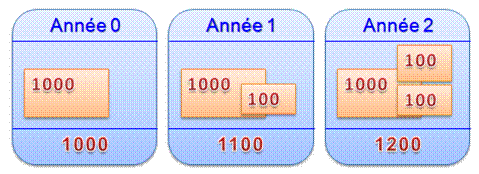
Que deviennent 1000 euros placés à 10 % ? Formule fondamentale

Capital plus intérêts au bout de deux ans: 1200 euros

Note: t est le taux en % comme par exemple 5 pour 5%, d'où la division par 100.

Intérêt simple
Je dispose d'une somme d'argent (capital) que je dépose à la banque pour que celui-ci me rapporte des intérêts. L'intérêt est la somme d'argent que la banque me versera pour chaque 100 euros de capital placé, et cela chaque année. Un intérêt simple veut dire que chaque année la banque me verse les mêmes intérêts sur le capital de départ. Pour trouver la somme des intérêts (SI) au bout de p années, il suffit de multiplier les intérêts d'une année par le nombre d'années. La somme disponible en fin de placement et égale au capital initial auquel on ajoute les intérêts.	Capital: C = 10 000 € Intérêt: t = 5% À la fin de l'année, la banque me verse des intérêts d'un montant de: I = C . t = 10 000 x 5% = 10 000 x 5 / 100 = 500 € En effet, dans 10 000, il y a 100 tranches de 100 et chacune me rapporte 5 euros. Avec un intérêt simple, je gagne 500€ d'intérêts tous les ans. Soit pour 10 ans: SI = C . t . p SI = 10 000 x 5% x 10 = 5 000 € Alors, je dispose de mon capital et de mes intérêts C + SI = 10 000 + 5 000 = 15 000 €

Exemples Capital: 400 € placé pour 5 ans à 6%. Capital: 3 650 € placé pour 125 jours à 8%. Capital: à trouver? 5,5 ans à 3,5% Intérêts: 350 €. Capital: 500 € 1 an et 8 mois à taux ? Intérêts: 33,33 €. Capital: 600 € sur 2 ans et 150 € sur 4 ans à un taux? Intérêts totaux: 90 €.

SI = 400 x 6% x 5 = 120 € SI = 3 650 x 8% x 125 / 365 = 100 € 350 = C x 3,5% x 5,5 C = 350 / 0,1925 = 1818,18 € 33,33 = 500 x t x 1, 666 t = 33,33 / 833,33 = 0,04 = 4% 600 sur 2 ans = 1 200 sur 1 an 150 sur 4 ans = 600 sur 1 an Total équivalent 1 800 sur 1 an 90 = 1 800 x t x 1 t = 90 / 1800 = 0, 05 = 5%

Exercices
Capital 1000 euros placés à 10% pendant 150 jours. Quels sont les intérêts perçus?	1000 x 150/365 x 10/100 = 41,10 euros
Capital placé sur un nombre d'années égal au taux d'intérêt. L'intérêt tiré est égal à 1/9 du capital. Quel est le taux?	C/9 = C. t . t / 100 t² = 100 / 9 t = 10 / 3 = 3,33%
Le capital investi double en 10 ans. Quel est le taux d'intérêt simple?	Hypothèse: capital = 100 Intérêt = 200 – 100 = 100 SI = 100 = 100 x 10 x t/100 t = 10 %
Le capital investi triple en 20 ans. Quel est le taux d'intérêt simple?	Hypothèse: capital = 100 Intérêt = 300 – 100 = 200 SI = 200 = 100 x 20 x t/100 t = 10 %
Le capital investi est multiplié par k en p années. Quel est le taux d'intérêt simple?
Placé à 5%, combien d'années pour quatre fois le capital?	P = 100(4 – 1) / 5 = 300 / 5 = 60 ans
Capital de 1000 euros divisé en trois parts, investies sur 2, 3 et 4 ans avec un taux simple à 5%. Valeur de chaque part pour un même rendement?	Intérêts SI1 = C1 x 2 x 5/100 = 0,1 C1 SI2 = C2 x 3 x 5/100 = 0,15 C2 SI3 = C3 x 4 x 5/100 = 0,2 C3 Capital acquis, tous égaux 1,1 C1 = 1,15 C2 = 1,2 C3 Somme C1 = 348 C2 = 333 C3 = 319

EMPRUNTS – 1000 euros à 5% sur 3 ans
Emprunts avec intérêts simples. On se propose de calculer le montant des remboursements (R) constants chaque année. Plusieurs cas selon que: les intérêts sont comptés plein pot ou dégressifs au fur et à mesure des versements; le prêteur souhaite encaisser les intérêts (souvent) ou vous faire profiter des intérêts (rare!); la première année produit des intérêts ou non; ou les versements se font à échéance début ou fin d'année.
Le prêteur offre les intérêts Avec intérêts complets Le prêteur impose le paiement des intérêts sur la somme totale durant la période. Il ne tient pas compte des remboursements qui diminue la dette.		Dette complète 1000 + 1000 x 5 x 3/100 = 1 150 euros Versement annuel 1 150 / 3 = 383,33 euros
Avec intérêts dégressifs Le prêteur accepte une dégressivité des intérêts au fur et à mesure des remboursements de la somme empruntée. Note: Avec un emprunt et intérêts complets, le versement annuel est de 383,33 euros; en tenant compte des sommes versées, diminuant le montant de la dette, les versements passent à 365 euros.	La dette est égale à la somme empruntée (E) augmentée des intérêts. Calculons les intérêts Première année Intérêts: E . t Versement: X Reste de l'emprunt à rembourser : E – X Deuxième année Intérêts: (E – X) . t Versement: X Reste de l'emprunt à rembourser : E – 2X Troisième année Intérêts: (E – 2X) . t Versement: X Reste de l'emprunt à rembourser : 0 Total emprunt et intérêts E + E.t + (E – X)t + (E – 2X)t = 3X

Le prêteur offre les intérêts Avec intérêts dégressifs Le prêteur vous prête une somme d'argent et, empochant vos versements et en les faisant fructifier. Il considère que les intérêts qu'il touche viennent dégrever votre dette.

Calcul des intérêts La dette est remboursée par 3 versements de X euros. Le versement en fin de la première année, placé à t % sur les deux années qui restent produit des intérêts de: 2 X . t Le versement X en fin de deuxième année produit des intérêts sur un an seulement, soit: X . t Bilan J'aurais dû payer 1000 euros. Cadeaux des intérêts: 2 X . t + X . t = 3 X . t Réglé par 3 versements: 3X D – 3 X . t = 3 X

Formulation générale X: versement annuel pendant p années D: dette théorique T: taux d'intérêt simple

ENGLISH CORNER
Interest is the money paid by the borrower to the lender for use of money lent. Interest Is usually calculated at the rate of so many euros for every 100 euros of the money lent for a year. This is called the rate per cent per annum or the rate per cent. The sum lent is called the principal. The sum of the principal and interest is called the amount. Interest is of two kinds, simple and compound.

Voir	Intérêts composés Intérêts – Toutes les formules Fraction Règle de trois
Aussi	Indicateurs économiques Économie Budget Patrimoine CAC 40 Crise de 2008 Nombres décimaux / fractionnaires
Sites	Intérêts – Wikipédia Analyse financière - Leçon 10 - Les Calculs d'intérêts (1/2) – ABC Bourse Intérêts – Université Paul Valéry
Livre	Magical book on quicker maths – M. Tyra – BSC publishing - 2000
Cette page	http://villemin.gerard.free.fr/aEconomi/aaaFINAN/Interet.htm