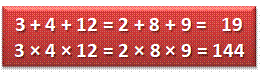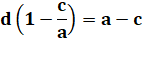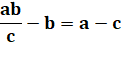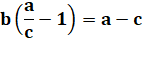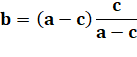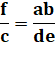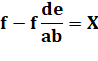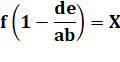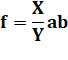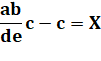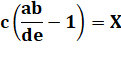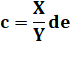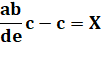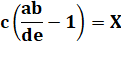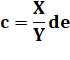|
Édition du: 24/05/2025 |
|
INDEX |
Égalités |
|||
|
S1 = S2 & P1 = P2 avec nombres |
Sommes et Produits avec
diviseurs S1 = S2 & P1 = P2 avec diviseurs |
|||
![]()
|
NOMBRES RECENSEURS Égalités entre SOMMES et entre PRODUITS de
nombres
Recherche
raisonnée: elle nécessite un peu d'astuce en présence de somme et de produit,
mais vite complexe avec de grands nombres. La solution
informatique s'impose. |
||
|
|
Sommaire de cette page >>> Cas de deux couples >>> Cas de deux triplets >>> Liste de solutions |
Débutants Glossaire |
Anglais: Census-Taker Numbers
(CTN)
À la base une énigme célèbre et déroutante
|
Énigme des trois filles Un dialogue succinct entre deux personnes et
l'âge des trois filles peut être déterminé. Énigme résolue du
fait de la propriété singulière du nombre 36 |
Nombre 36 Deux triplets de nombres (des diviseurs de 36)
ont même somme (S) et même produit (P)
|
|
Construction avec ces triplets Deux parallélépipèdes
ayant
|
|
Voir Nombre
36
|
On
établit l'égalité de base et on en déduit deux égalités qui vont servir pour
la suite. |
a + b = c + d ab = cd |
d – b = a – c
|
|
|
On
calcule à partir de la première équation en remplaçant b pas sa valeur
(colonne de gauche), puis d par sa valeur (colonne de droite). On
calcule. La
réponse est sans appel. Seule possibilité les couples sont égaux. |
d = a |
b = c |
|
|
Même
procédé de résolution que ci-dessus. On cherche
à exprimer deux variables à partir des quatre autres. |
a + b + c = d + e + f abc = def |
f – c = a + b – d – e = X
On note Y = ab – de |
|
|
Le
calcul montre qu'il existe toujours
une solution rationnelle (fraction). |
|
|
|
|
Exemple fractions a = 2, b
= 3, d = 4 et e = 5 |
X = -4 et
Y = -14 c= 40/7 et f = 12/7 |
2 + 3 + 40/7 = 75/7 4 + 5 + 12/7 = 75/7 2 x 3 x 40/7 = 240/7 4 x 5 x 12/7 = 240/7 |
|
|
Exemple entiers a = 2, b
= 3, d = 10 et e = 9 |
X = -14 et Y = -84 c = 15 et f = 1 |
2 + 3 + 15 = 20 10 + 9 + 1 = 20 2 x 3 x 15 = 90 10x 9 x 1 = 90 |
|
|
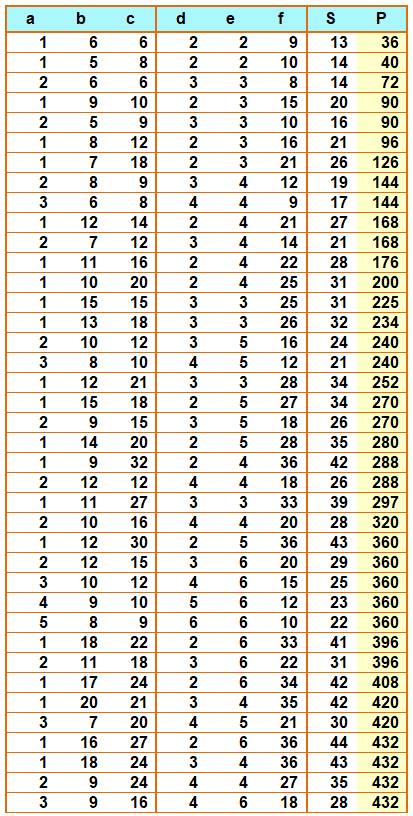
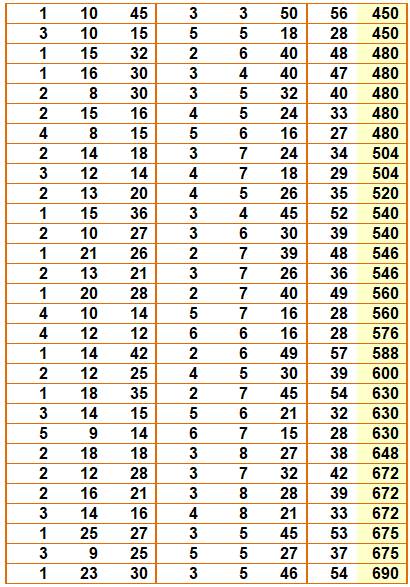
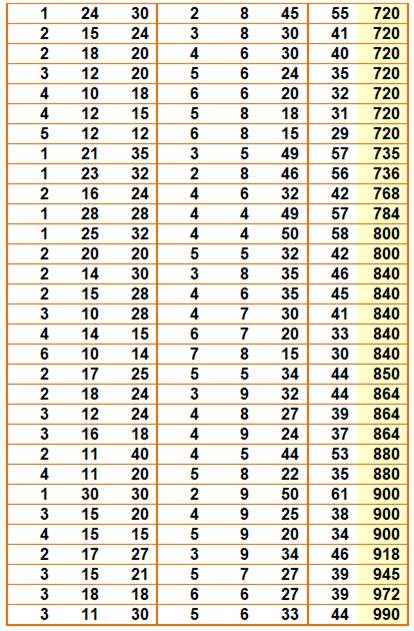
Solutions pour Exemple (première ligne) S = 1 + 6 + 6 = 2 + 9 + 2 = 13 P = 1 x 6 x 6 = 2 x 9 x 2 = 36 Liste des 54 valeurs de P jusqu'à
1000 {36, 40, 72, 90, 96, 126, 144, 168, 176, 200, 225, 234, 240, 252, 270,
280, 288, 297, 320, 360, 396, 408, 420, 432, 450, 480, 504, 520, 540, 546,
560, 576, 588, 600, 630, 648, 672, 675, 690, 720, 735, 736, 768, 784, 800,
840, 850, 864, 880, 900, 918, 945, 972, 990} Propriétés Les produits sont majoritairement pairs. Produits impacts dans cette
liste: 225, 297, 675, 735, 945. On aime aussi les "vrais" produits, sans le facteur 1. Alors
le premier représentant est 72. On aime particulièrement les triplets à nombres
distincts (c'est-à-dire: avec les diviseurs propres) comme 144, 168, …) Nombres
recenseurs (CTN) Pour ces nombres soient de vrais nombres recenseurs, et (donc) soient compatibles
avec la résolution de l'énigme, il ne doit exister qu'une
seule paire de triplets. Liste dont nombres impairs 225, 297, 735, 855, 945, 1275, 1701, … |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |