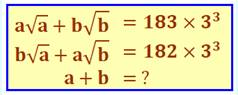Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/02/2024 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100 / 200			300 à 399			400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	300	310	320		330	340		350	360	370	380	390
	360	361	362		363	364		365	366	367	368	369

Un pays qui produit plus de 365 sortes de fromages ne peut pas perdre la guerre ! Charles de Gaulle

Voir Pensées & humour

Trois-cent-soixante-cinq

Three hundred sixty five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0110 1101
Bases	5558 1C114
Romain	CCC LX V

Suite

Composé

Congruent

Déficient

Docile (amenable)

Heureux

Impair

Palindrome binaire

Semi premier

Géométrique

Carré centré (14)

Chiffres et numération

365 = 5x8^2 + 5x8^1 + 5x8^0 = 5558	Valeur de ce nombre en octal.
365 – (3 + 6 + 5) = 351 = T26	Devient triangulaire en le diminuant de ses chiffres.
365 = 6! / (5 – 3) + 5	Opération avec les chiffres de 365.

Addition et soustraction

365 = 32 + 33 + … + 41

Une des trois sommes de nombres consécutifs >>>

Multiplication et division

365 = 5 x 73 1, 5, 73, 365	Facteurs Diviseurs
365 = 7 x 52 + 1	Explique que 1^er janvier et 31 décembre tombent le même jour de la semaine pour une année normale.
365 x 137 = 50005 365 x 64254 = 23452345 365 x 273863 = 99959995	Produits à chiffres répétés. Propriété: 365 = 5 x 73 et 73 x 137 = 10001 Objet de motifs sans fin comme ceux présentés. 99959995 est le plus grand motif avec répétition de quatre chiffres.
Tous les nombres en abc0 abc0 et abc5 abc5	sont divisibles par 5, 73, 137, 10 001, et 685, 365, 50005
365 Période d'aucun nombre connu.	On ne connait aucun premier avec une période égale à 365, alors que c'est le cas pour tous les nombres inférieurs. Entre 360 et 370, et pour p jusqu'à 130 000, on trouve seulement: Période 362 avec p = 13 757, Période 366 avec p = 367, Période 367 avec p = 3 671, et Période 367 avec p = 129 919
365 mod 2 à 12 = {1, 2, 1, 0, 5, 1, 5, 5, 5, 4, 5}	Restes de la division de 365 par les nombres de 2 à 12.
365 / 7 = 52,142857 142857… 365, 242 189 8 / 7 = 52,1774556857142857142857 …	Année calendaire divisée par quantité de jours dans la semaine. Même division avec durée de l'année tropique.

Avec les puissances

365 = 2 x 182 + 1 = 183² – 182²	Propriété générale des nombres impairs.
365 = 2² + 19² = 13² + 14² = 169 + 196	Deux seules sommes de deux carrés >>> Solution du système d'équations:
365 = 10² + 11² + 12² = 13² + 14² = 100 + 121 + 144 = 169 + 196	Unique telle sommes de carrés de nombres consécutifs. Joli motif! Plus petit nombre étant deux fois somme de carrés consécutifs. Motif qui se reproduit en commençant avec un nombre hexagonal du 2^e ordre.
365 = 2^3 + 2^3 + 2^3 + 5^3 + 6^3 = 3 x 2^3 + 6^3 + 5^3	Somme de cubes.

Culture

Maths	365 nombre de démonstrations recensées du théorème de Pythagore	>>>
Temps	365 ou 366 Nombre de jours dans l'année calendaire.	>>>
	365, 242 189 8 … j 365j 5h 48 mn 45, 96768 … s Année moyenne ou tropique. Période de révolution de la Terre.	>>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 1, 1, 0, 1, 1, 0, 1] 3, [1, 1, 1, 1, 1, 2] 4, [1, 1, 2, 3, 1] 5, [2, 4, 3, 0] 6, [1, 4, 0, 5] 7, [1, 0, 3, 1] 8, [5, 5, 5] 9, [4, 4, 5] 10, [3, 6, 5] 11, [3, 0, 2]	12, [2, 6, 5] 13, [2, 2, 1] 14, [1, 12, 1] 15, [1, 9, 5] 16, [1, 6, 13] 17, [1, 4, 8] 18, [1, 2, 5] 19, [1, 0, 4] 20, [18, 5] 21, [17, 8]	22, [16, 13] 23, [15, 20] 24, [15, 5] 25, [14, 15] 26, [14, 1] 27, [13, 14] 28, [13, 1] 29, [12, 17] 30, [12, 5] 60, [6, 5]	8, [5, 5, 5] 72, [5, 5] 364, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombres en 350 Nombres en 370
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb300/Nb365.htm