|
Édition du: 09/04/2025 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
|
![]()
Chiffres et numération
|
330 |
|
Addition
et soustraction
|
330 =
7 + 8 + … + 26 |
|
|
330 = 163 + 167
=
43 + 47 + 53 +
59 + 61 + 67 |
|
|
330 = 1x2 + 2x3 + …+
9x10 |
|
|
330 /
66 = 5 |
|
|
|
|
|
|
|
330,
331, 661, 991, 1321 1530,
1531, 3061, 4591, 6121 |
Liste: 330, 1530, 3060, 4260, 4950, 6840, 10830,
15390, 18120, 23010, 25410, 26040, 31770, 33300, 40110, 41490, 45060, 49830,
53880, 59340, 65850, 70140, 73770, 78540, 88740, 95460, 96930, … OEIS A237189 |
|
|
|
Liste des nombres : 330, 335, 340,
350, 355, 360. |
Avec les
puissances
|
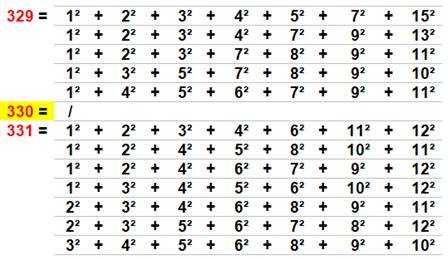
330 = 4² + 5² + 17² |
||
|
330 = 6² + 7² + 8² +
9² + 10² |
|
|
|
330 = 4² + 5² + 17² = 5² + 7² + 16² |
|
|
|
330 = 23 +
23 + 43 + 53 + 53 |
||
|
|
Voir
Nombre
390 Précédents: 318, 306, 286, 282, 266,
261, 258, 255, 253,250, 249 … |
|
En puissance
|
3303 = 113 + 123 + … + 1093
= 35 937 000 |
|
Jeux & Combinatoire
|
|
|
|
|
330 |
|
|
Culture
|
|
||
|
Transport |
Mis
en service en 1994; autour de 300 places. |
|
|
|
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 0, 0, 1, 0, 1, 0] 3,
[1, 1, 0, 0, 2, 0] 4,
[1, 1, 0, 2, 2] 5,
[2, 3, 1, 0] 6,
[1, 3, 1, 0] 7,
[6, 5, 1] 8,
[5, 1, 2] 9,
[4, 0, 6] 10,
[3, 3, 0] 11,
[2, 8, 0] |
12,
[2, 3, 6] 13,
[1, 12, 5] 14,
[1, 9, 8] 15,
[1, 7, 0] 16,
[1, 4, 10] 17,
[1, 2, 7] 18,
[1, 0, 6] 19,
[17, 7] 20,
[16, 10] 21, [15, 15] |
22,
[15, 0] 23,
[14, 8] 24,
[13, 18] 25,
[13, 5] 26,
[12, 18] 27,
[12, 6] 28,
[11, 22] 29, [11, 11] 30,
[11, 0] 60,
[5, 30] |
21,
[15, 15] 29,
[11, 11] 32,
[10, 10] 54,
[6, 6] 65,
[5, 5] 109,
[3, 3] 164,
[2, 2] 329,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()