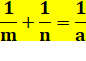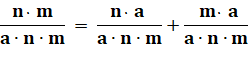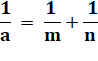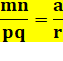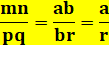|
Édition du: 06/06/2025 |
|
INDEX |
HEPTAGONE |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Heptagone régulier dans un cercle Démontrer une
propriété de proportions sur deux sécantes quelconques passant pas les
sommets de l'heptagone. |
||
|
|
Sommaire de cette page >>> Diagonales de l'heptagone >>> Heptagone dans cercle |
Débutants Glossaire |
|
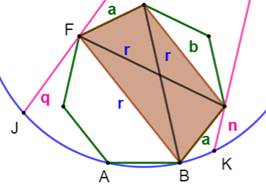
Propriété Dans l'heptagone régulier, démontrer la relation
suivante:
Démonstration Théorème de
Ptolémée dans le quadrilatère inscrit
ACDE: |
|
|
|
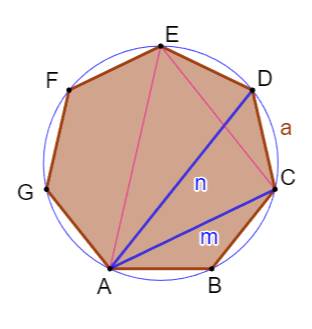
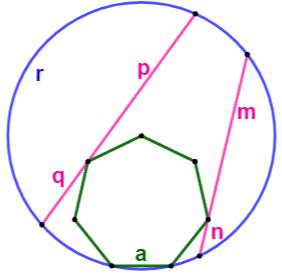
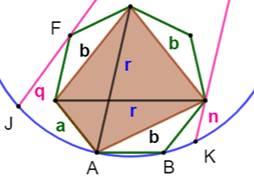
Construction Un heptagone
régulier (vert). Un cercle centré sur un des sommets de
l'heptagone et passant par les deux sommets opposés. Deux sécantes quelconques passant par les sommets
indiqués sur la figure. Démontrer la propriété indiquée. Pistes Les produits mn et pq font penser au théorème de
la puissance
des cordes. Chacun de ces produits est une constante quelle que soit la
sécante. Pour la corde mn, on invoque le théorème
de Stewart dans un triangle. Pour comparer ces produits au rayon du cercle et
au côté de l'heptagone, nous allons aussi chercher des relais à l'intérieur
de l'heptagone à l'aide du théorème de
Ptolémée concernant les diagonales d'un quadrilatère inscrit. |
Propriété
|
|
|
Puissance de la corde pq Le théorème s'applique à deux cordes sécantes. On connait les quatre longueurs sur les cordes.
|
|
|
|
Théorème de Stewart dans le
triangle EIK On note b, la longueur d'une diagonale courte de
l'heptagone. Application du théorème de Stewart:
|
|
|
|
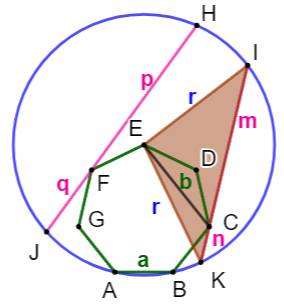
Théorème de Ptolémée dans les
quadrilatères colorés Ces quadrilatères, construits sur les sommets d'un
polygone régulier sont inscriptibles: leurs quatre sommets sont sur un
cercle. Notez que les diagonales de l'heptagone sont
égales à b pour les plus courtes et à r pour les plus longues. Quadrilatère du haut:
Quadrilatère du bas:
|
|
|
|
Rapprochement des résultats |
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/HeptaCer.htm
|