Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 03/07/2021 M'écrire Brèves de Maths

INDEX Cercle Géométrie	Apollonius – Constructions
	Cercle d'Apollonius		Trois cercles d'Apollonius
	PPP (1)	PLL 4)		LLL (3)	CCC (10)
	PPL (2)	PLC (6)		LLC (5)
	PPC (8)	PCC (9)		LCC (7)

Construction d'Apollonius Trois cercles (CCC) Comment construire un cercle tangent à trois cercles. Il s'agit du dixième problème d'Apollonius. Il a été résolu par François Viète en s'appuyant sur la résolution des cas précédents. Il avait habilement utilisé les méthodes classiques de la géométrie euclidienne. Les constructions modernes recourent plutôt à la géométrie des inversions ou à la géométrie analytique. Méthodes plus efficaces mais moins accessibles aux profanes. Cette page propose une approche générale. On ne traite pas des cas particuliers conduisant à des d'impossibilités. On commence par traiter des configurations simples de deux ou trois cercles.
	Sommaire de cette page >>> Cas de trois cercles identiques >>> Cas de trois cercles dont deux identiques >>> Cas de deux cercles tangents >>> Cas de trois cercles tangents >>> CCC: Les huit solutions >>> Cas de trois cercles – Méthode de Viète	Débutants Triangle Géométrie Glossaire Triangle

Cas de trois cercles identiques		haut
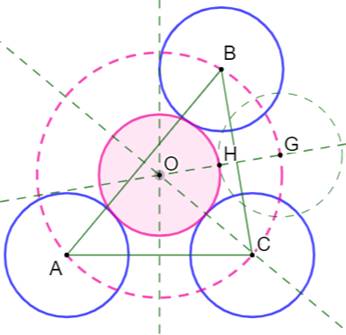
But Construire le cercle tangent à trois cercles disjoints mais de même rayon. Construction Trois cercles (bleus) de rayon r. Le cercle passant par les trois centres (pointillés roses). Son centre est le point de rencontre des trois médiatrices des côtés. Intersection G entre une médiatrice et le cercle en pointillés. Cercle (G, rayon r). Intersection H avec la médiatrice. Cercle (O, OH) qui est le cercle cherché (rose). Commentaires Point O: centre du cercle circonscrit au triangle et du cercle cherché Rayon cherché: rayon circonscrit moins rayon cercles initiaux.

Cas de trois cercles dont deux identiques		haut
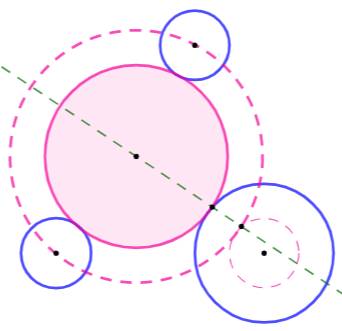
But Construire le cercle tangent à trois cercles disjoints dont deux de même rayon. Construction Deux cercles (bleus) de rayon r et un de rayon R. Cercle concentrique au plus grand et de rayon r. Construction PPC du cercle rose en pointillés. Construction du cercle concentrique de même rayon moins r. C'est le cercle cherché (rose).

Cas de deux cercles tangents		haut
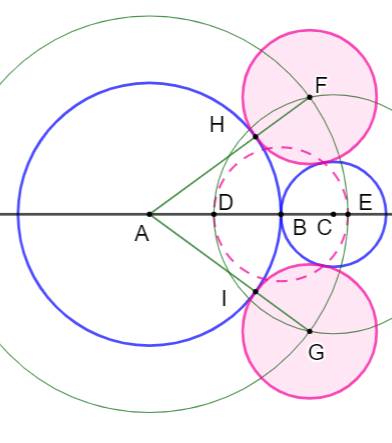
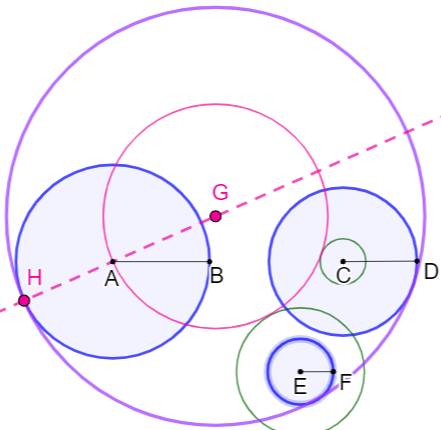
But Construire les deux cercles roses tangents aux deux cercles bleus, eux-mêmes tangents. Construction Cercles bleus de centre A et C et tangents en B. Cercle de centre B et de rayon quelconque (pointillés roses). Intersections D et E avec AC. Cercles (A, AE) et (C, CD). Intersections en F et G. Segments AF et AG. Intersections en H et I. Cercles (F, FH) et (G, GI) qui sont les deux cercles solutions du problème.

Cas de trois cercles tangents		haut
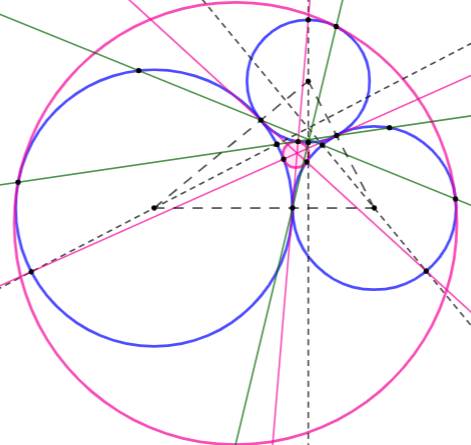
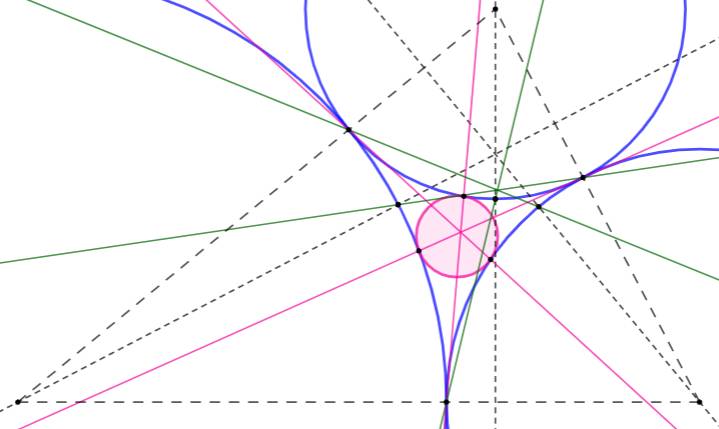
But Construire les deux cercles tangents à trois cercles mutuellement tangents Guide de construction Trois cercles initiaux en bleu. Le triangle avec les centres pour sommet et ses hauteurs (pointillés noirs). Les six intersections avec les cercles. En rose les droites reliant une de ses intersection avec le point de tangence opposé. Intersection avec un cercle. Les trois intersections sont les points de tangence du cercle cherché intérieur. Même chose avec les droites en vert pour l'autre cercle. Voir Théorème de Descartes (calcul des rayons)	Figure complète
Détail des intersections centrales

CCC: Les huit solutions pour trois cercles mutuellement externes

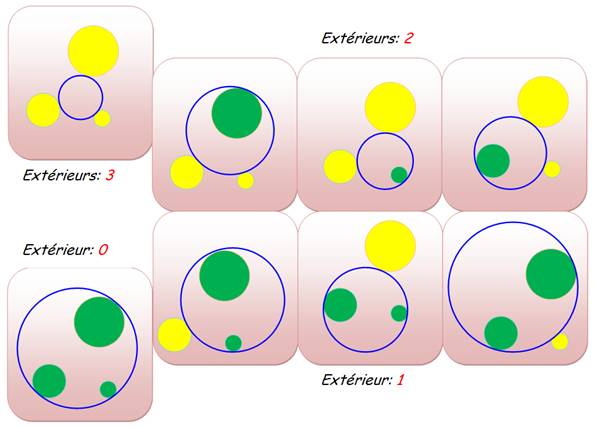
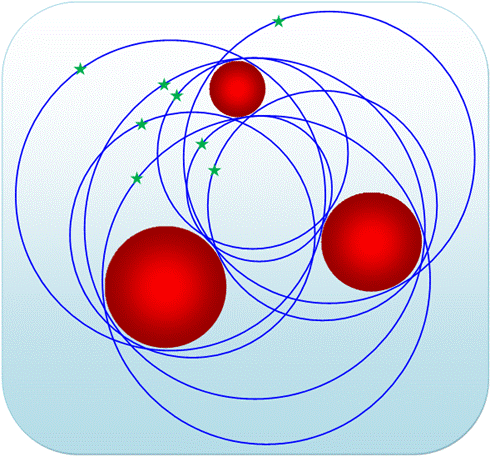
Soit trois cercles disjoints quelconques de rayons différents. Trouvez tous les cercles tangents aux trois cercles initiaux. Les huit cercles en bleu sont solutions. Chacun est tangent aux trois autres. Le dénombrement est simple en tenant compte de la quantité de cercles initiaux à l'extérieur (jaunes) et à l'intérieur (verts) du cercle tangent (bleu). En une seule figure (les huit étoiles vertes identifient chacun des cercles)

Cas de trois cercles – Méthode de Viète			haut
But Construire le cercle tangent à trois cercles disjoints. Guide de construction Trois cercles initiaux en bleu. Rayons: AB = r, CD = s, EF = t Cercle vert en C de rayon s + r ou r – s. Cercle vert en E de rayon t + r ou t – s. Les différentes possibilités conduiront aux huit cercles possibles. On est ramené à un problème connu: construction PCC avec le point A et les deux cercles verts. Ce qui conduit au cercle rose de centre G. Droite GA. Intersection H. Le cercle (G, GH) est le cercle cherché.
Démonstration complète Il serait sans doute difficile de montrer toute la démonstration de Viète en une seule figure. En effet, astucieusement, Viète trouve le moyen de résoudre un cas en s'appuyant sur les résultats de cas déjà traités. Ce procédé est décrit dans la Thèse d'Anne Boyé >>>		Problèmes d'Apollonius La résolution du n°1 permet celle du 8, puis du 9 et enfin celle du 10.

Haut de page

Retour	Construction d'Apollonius
Suite	Puissance d'un point Cercle – Index
Voir	Éléments remarquables du triangle Équation du 45^e degré résolue par Viète.
Sites	10. Un problème d'Apollonius: cercle tangent à trois cercles – Descartes et la Géométrie – Patrice Debart Utilisation de l'outil "Puissance": 4 - Un problème d'Apollonius : Cercles tangents à 3 cercles – Abra Cadabri – Jean-Marie Laborde L'Apollonius Gallus et le problème des trois cercles – Thèse d'Anne Boyé – 1998 – pdf 214 pages Efficiently constructing tangent circles – Arthur Baragar and Alex Kontorovich Tangencies: Apollonian Circles – The Geométry Junlyard The Tangency Problem of Apollonius – Décrit la méthode de Gergonne pour la construction des cercles tangents à trois cercles.
Livre	Apollonius Gallus - François Viète - Google Livre – En Latin
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/ApolCCC.htm