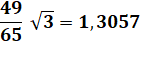|
|||||||||||||||||||||||||||||||||||||
![]()
|
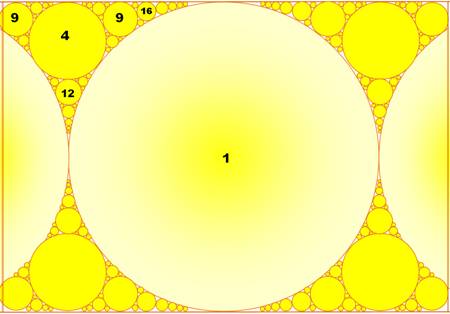
Baderne ou cercles d'Apollonius Ensemble de cercles tangents
inclus dans un cercle enveloppe, produisant une figure d'allure fractale. |
Anglais: Apollonius Circles
|
|
||
|
Baderne: grosse tresse de
marine qui sert à garnir les endroits à préserver du frottement ou de
l'humidité. Ici, il s'agit d'une figure fractale
construite en répétant sans fin le problème des contacts d'Apollonius. L'esthétique de la figure est
adaptée en choisissant judicieusement les cercles de départ (trois, quatre …)
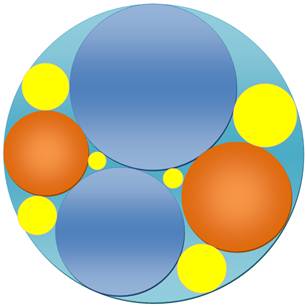
En haut en bleu les trois cercles de
départ; en ocre les deux seuls cercles tangent possibles; puis, les six
possibles (en jaune) à la troisième génération. Une des figures les plus classiques,
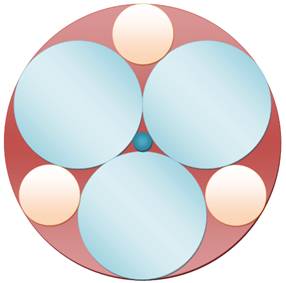
en bas, consiste à prendre trois cercles initiaux tangents et de même rayon
(en bleu clair). Dimension
fractale
Dimension
de Hausdorff des cercles
d'Apollonius. |
|
|
Anglais: Apollonian Gasket, Apollonian Net, Apollonius'
Gasket, Curvilinear Sierpinsky Gasket,
Soddy Circles, Kissing Circles,
Apollonian circle packing
Voir Cercle de Poincaré
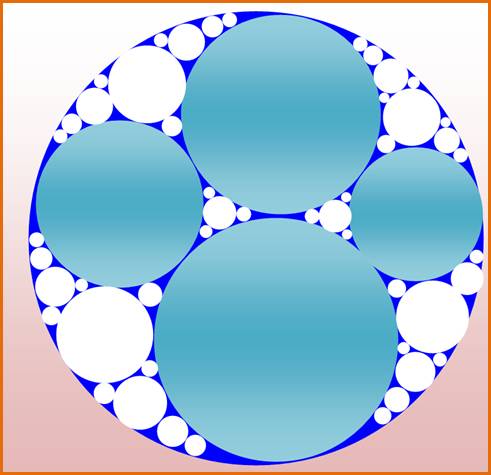
Une baderne dans le cas général
|
|
||
|
Quatre
cercles en configuration de Descartes Avec trois cercles quelconques et le cercle tangent
intérieur. Ou dit autrement, quatre cercles tangents mutuellement dont l'un est tangent intérieurement aux
trois autres: Si la courbure de chacun de ces quatre cercles est un nombre entier, alors la courbure
de chacun des cercles de la baderne est un nombre entier. Formule pour quatre cercles en configuration de
Descartes:
Si c est l'inconnu, alors deux valeurs possibles pour
cette équation du second degré.
Elles sont telles que: c1 + c2
= 2 (C + C' + C") Cette relation montre que les rayons de courbure c1
et c2 sont des nombres entiers si a, b et c le sont. Le cercle qui
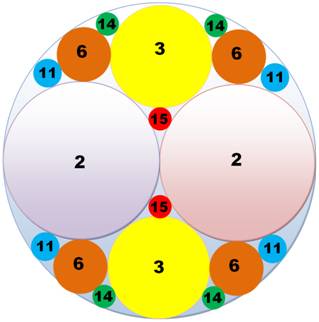
contient les autres sera associé à une courbure négative. Sur cette image en jaune, les quatre cercles initiaux
sont particuliers: deux cercles avec une courbure égale à 1 et deux cercles
avec courbure égale à 0, soit deux droites (cercle de rayon infini). Application Ce n'est
pas que des figures géométriques esthétiques. La présence de nombres entiers
est utilisée pour accélérer la recherche des nombres premiers par la méthode
des cribles améliorés
(méthode du cercle). |
Les nombres
entiers qui figurent ici sont les valeurs de la courbure
(inverse du rayon) de chacun des cercles. La courbure du plus grand cercle
étant égale à 1.
Cette baderne
a été obtenue avec quatre cercles mutuellement tangents dont eux sont des
cercles de rayon infini, soit les deux droites parallèles en haut et en bas. |
|
Galerie
|
|
Sources:
Voir les sites indiqués ci-dessous.
Pour
ces images complètes et d'autres mettre "Apollonian gasket" dans un
moteur de recherche
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()