|
Édition du: 27/06/2021 |
|
INDEX |
Apollonius – Constructions |
||||
|
PPP (1) |
PLL 4) |
LLL
(3) |
CCC (10) |
||
|
PPL (2) |
PLC (6) |
LLC (5) |
|||
|
PPC (8) |
PCC (9) |
LCC (7) |
|||
![]()
|
Construction d'Apollonius Deux points et une droite (PPL) Comment
construire un cercle tangent à une droite et passant par deux points ? Cette page propose une approche générale. On
ne traite pas des cas particuliers conduisant à des d'impossibilités. |
||
|
|
Sommaire de cette page >>> Un point, une droite >>> Cas de AB parallèle à la droite >>> Deux points, une droite – Méthode 1 >>> Solution >>> Deux points, une droite – Méthode 2 >>> Deux points, une droite – Méthode 3,
inversion |
Débutants Glossaire |
|
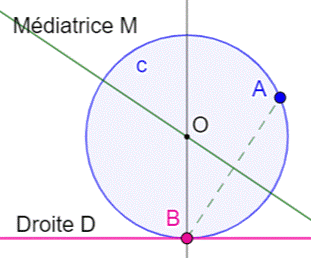
But Construire le cercle
tangent à la droite D au point B et passant par le point A. Construction Perpendiculaire
en B à la droite D. Segment AB. Médiatrice de AB
(verte). Intersection O,
centre du cercle cherché. |
|
|
|
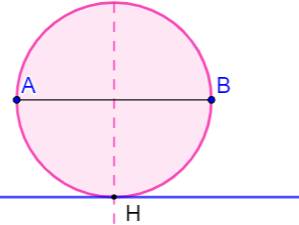
But Construire le
cercle tangent à la droite D et
passant par les point A et B avec AB parallèle à la droite D. Construction Médiatrice de
AB. Intersection avec
la droite D en H. Cercle circonscrit
aux trois points A, B et H. |
|
|
|
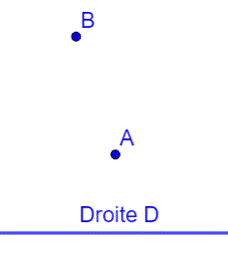
But Construire le cercle tangent à la droite D
passant par les points A et B. |
|
|
|
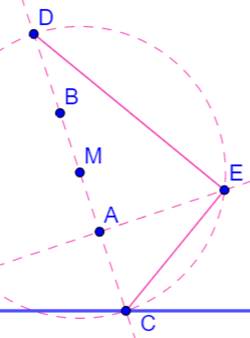
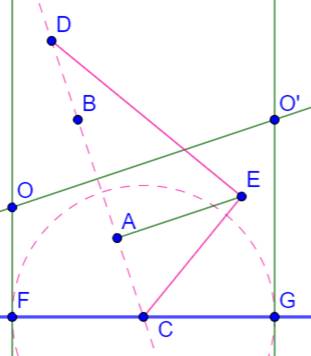
Construction Droite AB. Intersection avec D en C. BD = AC M milieu de AB (et aussi de CD). Cercle (M,
MC). Perpendiculaire en A à AB. Intersection en E avec le cercle |
|
|
|
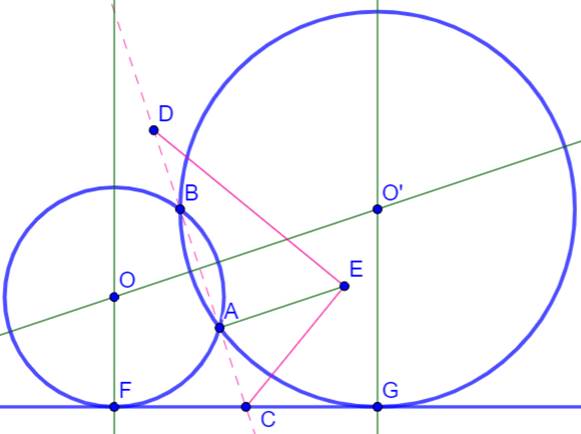
FC = CG =
AE Perpendiculaires en F et G à la droite D. Médiatrice de AB. Intersections en O et O', les centres des deux
cercles cherchés. |
|
|
Les deux cercles tangents à la droite D et
passant par A et B
|
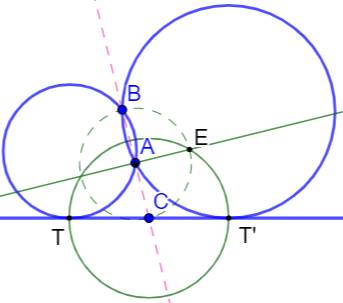
But Construire le cercle tangent à la droite D
passant par les points A et B. Construction Construire le point C, intersection de AB et D. Cercle de diamètre BC (pointillés verts, le
centre n'est pas A). Perpendiculaire en A à AB. Intersection E. Cercle (C, CE) (vert). Intersections en T et T', les points de tangence des
deux cercles cherchés (bleus). |
|
|
Voir
Construction par méthode de l'inversion >>>
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://users.math.uoc.gr/~pamfilos/eGallery/problems/Power