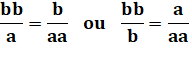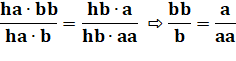|
Édition du: 15/01/2020 |
|
INDEX |
Géométrie – RECTANGLES |
||
![]()
|
Parallélogramme et TRIANGLE Énigme de comparaison des aires |
||
|
|
Sommaire de cette page >>>
Comparer les aires – Problème >>>
Comparer les aires – Solution |
Débutants Glossaire |
|
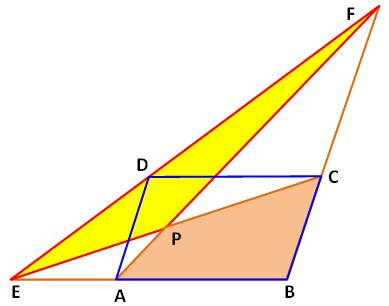
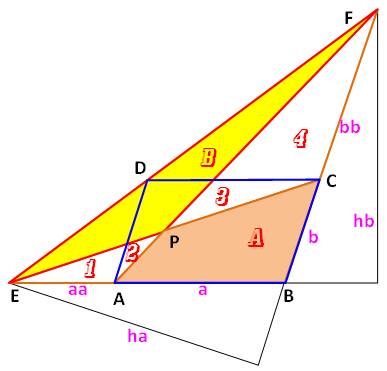
Énigme Un
parallélogramme ABCD. Un point
F quelconque sur la droite BC. FD coupe
AB en E. Tracer FA
et CE; intersection en P. Montrer
que l'aire jaune EFP est égale à l'aire ocre ABCP. |
|
|
|
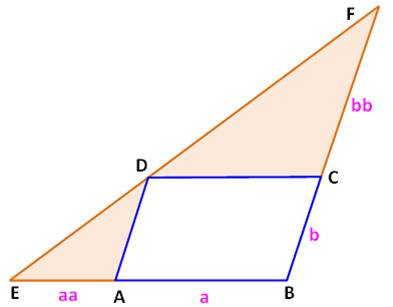
Indice Du fait que les côtés du parallélogramme sont
parallèles deux à deux, les triangles FDC et DEA sont semblables. On a donc cette proportion:
|
|
|
Voir Aire du
parallélogramme – Introduction et développements
|
Résolution Aire A = EBC – 1 – 2 = ABF – 3 – 4 Aire B = EAF – 1 – 2 = ECF – 3 – 4 Il faut démontrer que (aires): EBC= EAF ? ou ABF = ECF ? En évaluant les aires, il faudrait: ha.b = hb.aa
ou hb.a = ha.bb En divisant l'une par l'autre:
Or cette proportion est celle que nous avons
indiquée en indice: elle est vraie. En remontant, on démontre bien que les aires de
couleur sont égales. |
|
||
|
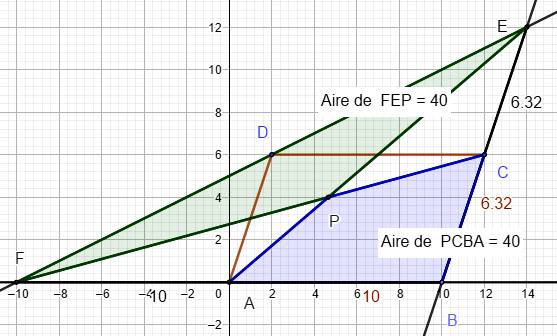
Illustration avec GeoGegra Configuration particulière où a = aa = 10. |
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |