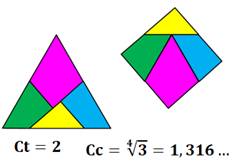|
Édition du: 23/06/2025 |
|
INDEX |
Dissections |
||
|
Carré-Triangle
équilatéral (problème du mercier) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Carré en triangle équilatéral Problème du mercier (haberdasher'
problem)
Comment
partager le carré
en un minimum de pièces telles que ces pièces assemblées forment un triangle
équilatéral ? En 1902,
Dudeney propose une solution en quatre pièces. En fin 2024, deux chercheurs japonais et
un américain démontrent que "quatre pièces" est bien le minimum
possible. |
||
|
|
Sommaire de cette page >>> Présentation >>> Construction >>> Résolution de la figure >>> Une construction approchée >>> Historique |
Débutants Glossaire |
|
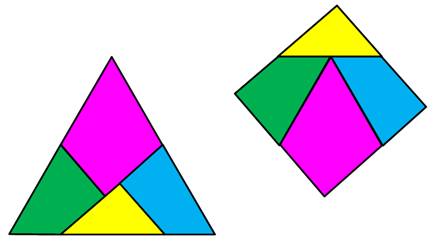
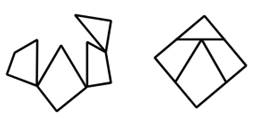
Passage du triangle au carré Le triangle équilatéral est partagé en quatre
pièces. Ces pièces sont réassemblées pour produire un
carré. Le quadrilatère
mauve reste en place. Les quadrilatères bleu et vert pivotent pour se
loger sur les flancs du quadrilatère mauve. Le triangle jaune monte en position de chapeau de
l'ensemble. |
|
|
|
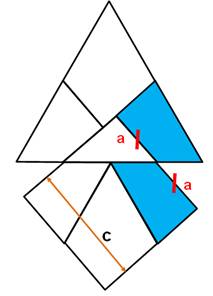
Carré et triangle réunis En gardant le triangle jaune en commun, il est possible
de réunir le triangle équilatéral et le carré en une seule figure. Taille du carré La figure de droite montre comment la pièce bleue
pivote pour passer du triangle au
carré. La mesure "a" est commune. Le côté du carré vaut: c = 2a. |
|
|
|
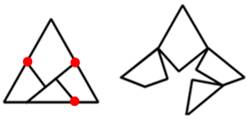
Articulation Les pièces peuvent être fixées par des pivots
(rouges) pour constituer un puzzle d'une seule pièce. On passe alors du triangle au carré et
réciproquement en ayant un seul objet dans les mains. |
|
|
|
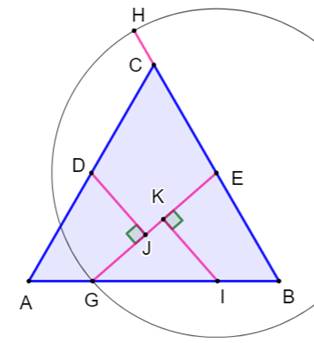
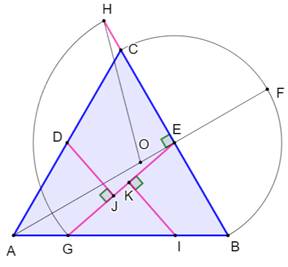
Étapes de construction Triangle équilatéral ABC. Milieux D et E des côtés AC et BC. Demi-droite AE. Demi-cercle BC. Intersection F. Milieu O de AF. Cercle (O, OA) Demi-droite BC. Intersection H. Cercle (E, EH). Intersection
G. Segment GI = BE. Perpendiculaire de D à GE. Intersection J. Perpendiculaire de I à GE. Intersection K. Nous disposons de la dissection du triangle. Rappel: c = 2a = 2 × IK |
|
|
|
Dimensions En partant d'un triangle de côté 2 cm, nous
allons montrer que le côté du carré sera
égal à la racine quatrième de 3, soit 1,316…. cm. Nous utiliserons le théorème
de Pythagore et la loi
des sinus dans le triangle. |
|
|
|
Calcul du côté du carré
|
Avec un triangle équilatéral de côté 2, le côté du carré est égal à
deux fois IK, soit c = racine quatrième de 3 = 1, 316… |
|
|
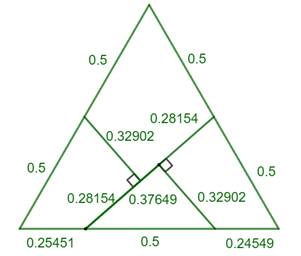
Dimension des pièces
|
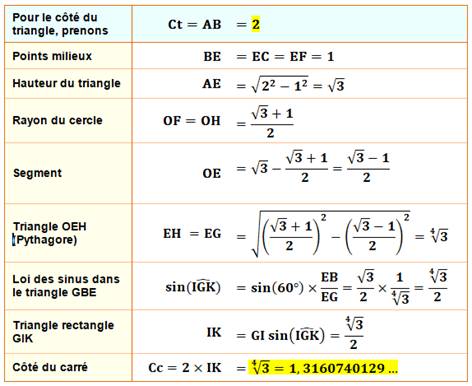
La table de gauche indique les formules de calcul pour chacune des
dimensions indiquées. |
|
|
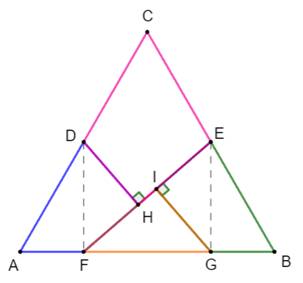
Constructions du triangle
équilatéral Un triangle équilatéral ABC de côté unité. Les milieux D et E des côtés AC et BC. Perpendiculaires en D et E au côté AB. Intersection en F et G. Segment FE Perpendiculaires en D et G au segment FE. Le triangle est ainsi découpé en quatre
polygones. |
|
|
|
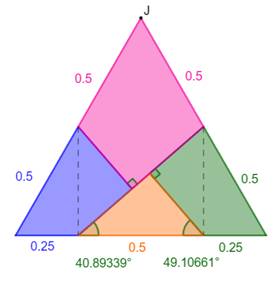
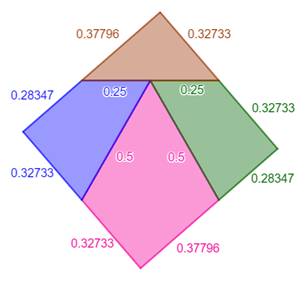
Le triangle équilatéral La figure montre la dissection du triangle
équilatéral en quatre polygones dont on donne quelques mesures. Le carré Il est évidemment formé des mêmes pièces. En maintenant la pièce rose immobile, on fait
pivoter les pièces bleue et verte autour des points milieux. Ces mouvements
aboutissent à l'esquisse d'un carré dont manque la pointe triangulaire. Justement, le triangle ocre y prend exactement sa
place. Construction approximative OUPS! Le
carré est un rectangle ! En effet, mesurons les côtés: Les côtés adjacents ne sont pas égaux. |
|
|
|
En 1902, Henry Ernest Dudeney propose la
dissection d'un triangle équilatéral en un carré et propose une solution en cinq
pièces puis en quatre pièces avec la connaissance sans doute d'une telle
solution que connaissait McElroy. En 1907, Dudeney publie la solution dans le livre
The Canterbury Puzzles sous le nom
de The haberdasher's Puzzle. " The problem is to cut an equilateral triangle into four pieces
that can be reassembled to form a square (without overlap and flipping, via
translation and rotation) " Le puzzle de Dudeney reste l'un des exemples les plus
célèbres de dissection géométrique. Au-delà de son attrait pour les mathématiciens,
les problèmes de dissection ont des applications pratiques dans des domaines
tels que la conception, l'ingénierie et la fabrication des textiles. Plus de 120 ans après la solution de Dudeney, une
question demeure : est-il possible de résoudre le puzzle avec moins de quatre
pièces ? |
La réponse est NON! Impossible avec moins de quatre pièces. En décembre 2024, grâce à une démonstration de 18
pages, des mathématiciens ont prouvé que la solution historique du puzzle de
Dudeney est bien la plus optimale. Il s'agit de deux chercheurs de l'Institut
japonais avancé des sciences et technologies (Uehara et Kamata) et un
chercheur (Demaine) du MIT (Massachusetts Institute of Technology,
États-Unis). La démonstration utilise des diagrammes de
correspondance (matching diagrams). Avec cette méthode, les différentes pièces
formant le triangle et le carré sont réduites à un graphe qui lie leurs côtés
et leurs sommets. Lorsque
deux polygones peuvent être disséqués l'un dans l'autre, il existe deux
relations de correspondance : l'une entre les sommets et l'autre entre les
bords des pièces. Ce sont ces relations qui sont analysées. La
référence de leur publication est donnée in fine. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |