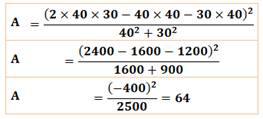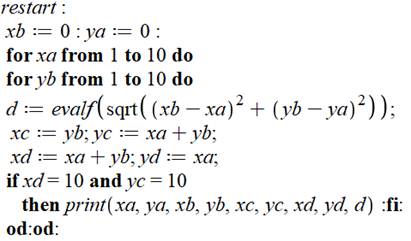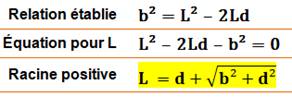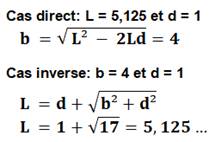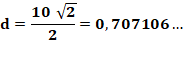|
Édition du: 18/10/2025 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Calcul de dimensions Quelle est la longueur du côté d'un carré inscrit
dans un carré
? Ou celle du carré origine, connaissant le côté du carré inscrit. Résolution de l'énigme du mur,
de l'échelle et du cube. Aussi, quelques petits défis de géométrie pour commencer cette page. |
||
|
|
Sommaire de cette page >>> Carré oblique au
milieu d'un carré >>> Taille du carré
oblique >>> Un problème et sa
difficulté >>> Carré inscrit dans
un quadrilatère >>> Aire des carrés >>> Carré inscrit dans
le carré – Taille minimale >>> Exercice avec un
carré inscrit dans un carré >>> Dimension du carré
inscrit >>> Carré
inscrit – Valeurs de x et y >>> Énigme de l'échelle
contre un mur >>> Bilan |
Débutants Glossaire |
|
Cas
simple avec démonstration quasi-muette. Construction Un
carré et les points milieux de ses côtés. Ceux-ci
sont joints deux à deux en oblique, créant une région centrale carrée. Quelle
est l'aire de ce carré central ? Piste On
"élargit le cadre" en construisant la même figure autour de la
figure initiale. Le
carré central se trouve entouré de quatre carrés identiques qui forment une
croix. Les
quatre triangles rectangles identiques qui débordent du carré initial sont
compensés par quatre triangles rectangles identiques internes au carré et qui
débordent de la croix. Solution L'aire
de la croix vaut 5 fois l'aire du carré central. En
reportant l'aire des triangles qui se compensent, c'est aussi l'aire du carré
initial. Aire
du carré central =
1/5 de l'aire du carré initial. |
Figure initiale
Figure pour solution
|
|
|
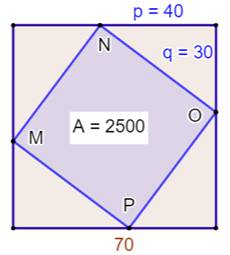
Carré oblique inscrit dans le carré Construction Un
carré de 70 cm de côté. Un
carré oblique dont les sommets sont situés sur les côtés du premier. Parmi
deux de ses côtés adjacents, l'un est situé à 30 cm et l'autre à 40 cm d'un
sommet commun du grand carré. Quelle
est l'aire du carré oblique ? Solution Vous
avez reconnu le célèbre
triangle rectangle de 30 cm et 40 cm qui, via le théorème
de Pythagore, offre une hypoténuse entière égale à 50 cm (30² + 40² =
50²). Le
côté du carré oblique mesure 50 cm et son aire est donc: 2 500 cm². |
|
|
|
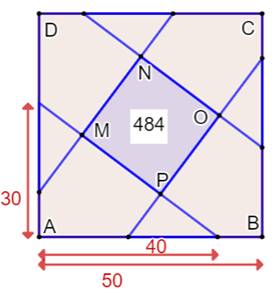
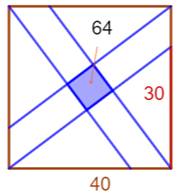
Carré oblique interne au carré Construction Un
carré de 50 cm de côté. Quatre
obliques, dont les extrémités de chacune sont situées sur le carré à une distance
de 30 cm pour l'une et 40 cm pour l'autre. Quelle
est l'aire du carré oblique ? Piste Cette
figure peut être vue comme un carré recouvert de quatre triangles rectangles
du type AMF (figure du
milieu). L'aire
du carré central MNOP est égale à celle du carré ABCD diminuée de celle des
quatre triangles rectangles et augmentée de quatre fois l'aire des petits
triangles comme LPF qui, du fait du recouvrement des triangles, sont comptés
deux fois. Calculs
|
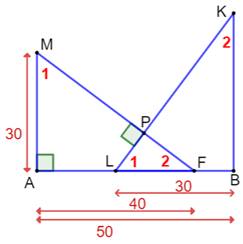
Les
triangles MAF et LFP sont semblables
car leurs angles sont égaux deux à deux (Voir
numérotation des angles). |
|
|
Calcul
littéral avec c le côté du carré et a, b pour les
distances au sommet
|
Exemple a = c = 40 et b = 30
Calculs numériques
|
|
|
|
||
|
Situation Un quadrilatère quelconque dont un
des sommets est C. Un carré inscrit dans ce quadrilatère dont un des côtés
est AB. Les segments de type AC (roses) sont
de même longueur. Dans ces conditions, montrer que le
quadrilatère est aussi un carré. Difficulté Pour démontrer cette propriété, on
pourrait penser considérer les quatre triangles du type ABC et montrer qu'ils
sont isométriques. Seulement, on ne connait que deux éléments
de ces triangles: AB et AC. Il n'est pas évident que les segments du type BC
soient de même mesure. Quant aux angles, on ne peut rien dire.
|
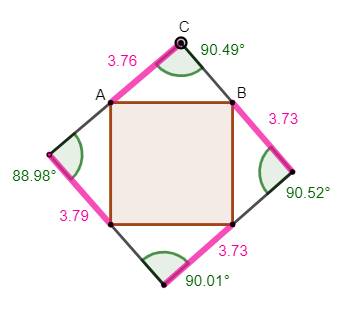
Un carré inscrit dans
un quadrilatère
Sur
cette figure approximative, il n'est pas évident de montrer que, si les
segments roses sont de mêmes mesures, les triangles du type ABC sont
isométriques. |
|
|
|
||||
|
Problème Carré ABCD (bleu), et EFGH (rouge)
un quadrilatère circonscrit tel que: AE = BF = CG = DH. Montrer que le quadrilatère EFGH
(rouge) est aussi un carré. Propriété utile
(lemme)
Solution L'astuce consiste à reporter le
triangle AHD en ABM. C'est une rotation autour de A; D passe en B et H en M.
Conséquence: AE = HD = BM. Angles:
DAB = 90° = DAM + MAB = DAM +
HAD = HAM = 90° Dans le quadrilatère AEBM, angle droit en A et AE = BM. On applique le
lemme: Idem pour les trois autres angles. Or la somme des angles du
quadrilatère doit atteindre 2 Chacun des quadrilatères comme AEBM
est un rectangle et EB = AM = AH. En ajoutant BF et AE, on a: EF = FG = GH =
HE. Avec quatre angles droits et des
côtés égaux, le quadrilatère EFGH est un carré.■ |
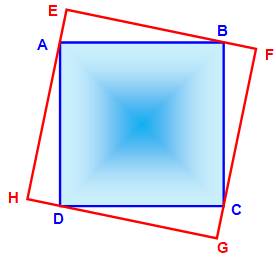
Figure initiale
Carré
bleu inscrit dans un quadrilatère rouge inconnu. AE = BF = CG = DH. Figure avec triangle
vert
Le quadrilatère
rouge est aussi un carré. |
|||
|
|
||
|
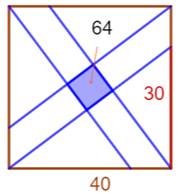
Problème Quelle est l'aire du carré rouge ? Solution La découpe présentée à droite donne la solution. |
|
|
|
|
||
|
Problème Quelle est la taille du carré inscrit d'aire
minimale ? Solution Pour minimiser l'aire du carré inscrit, il faut
maximiser l'aire des quatre triangles. Aire d'un des triangles rectangles: L'aire en fonction de a est une fonction parabolique
qui prend les valeurs extrêmes 0 et L. Son minimum est atteint au milieu: a =
(0 + L) / 2 = 1/2 L. |
L'aire du
carré inscrit (vert) est
minimale pour a = L/2 |
|
|
|
||
|
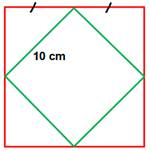
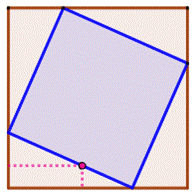
Problème Trouver toutes les valeurs entières pour
lesquelles le carré bleu est inscrit dans le carré rose. Écrire le programme et confirmer la position pour
un carré bleu d'aire minimale. Solution Le point A navigue sur l'axe en abscisses et le
point B en ordonnées. yA et xB valent
0. Inutile de faire intervenir les équations
des droites et leurs intersections dans le cas présent. Le point C se déduit par la relation: Le point D par: En faisant varier xA et yB, il s'agit de vérifier
si yC = 10 et si xD = 10. |
|
|
|
Programme Maple
|
Commentaires Initialisation. Boucle de balayage pour xA et yB. Calcul du côté d du carré. Calcul des coordonnées de points C et D Comparaison à 10 et impression des huit
coordonnées suivi de la distance. Résultats En
bleu, chaque ligne est un cas où le carré bleu est inscrit dans le carré
rose. En
fait, c'est le cas pour chacune des valeurs entières de xA de 1 à 9 (pour 10,
on retrouve le carré initial). Mieux,
il existe une infinité de tels carrés bleus. Le
plus petit (jaune) est obtenu pour A au milieu du côté du carré rose (xA = 5)
et le côté vaut: |
|
|
|
||
|
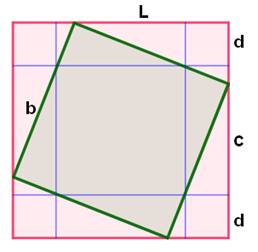
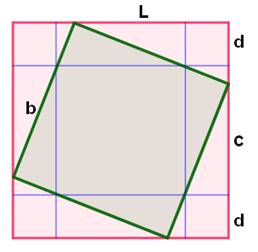
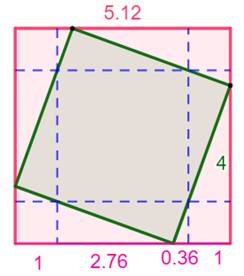
Problème Un carré rouge (côté L) dans lequel est inscrit
un carré vert (côté b) tel que celui-ci s'appuie sur un petit carré en coin
(côté d). Connaissant le point d'appui (d), trouver la
relation entre les côtés des carrés (L et b). Solution pour b = f(L)
Solution pour L = f(b)
|
Applications numériques
|
|
|
|
||
|
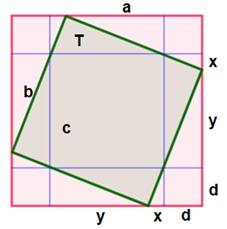
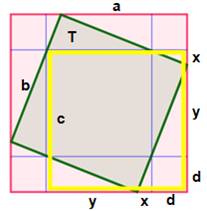
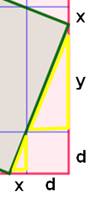
Problème Un carré rouge (côté a) dans lequel est inscrit
un carré vert (côté b) tel que celui-ci s'appuie sur un petit carré en coin
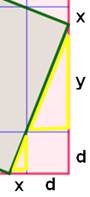
(côté d). Connaissant b et d, trouver les longueurs x et y. Solution (voir
figures du milieu)
|
Figure et notations (T est une
aire)
Grand latéral et triangle
semblables
Application numérique (proportions
rspectées) |
|
![]()
|
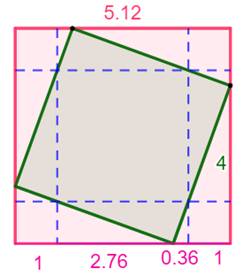
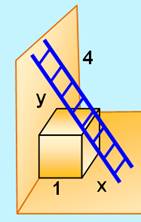
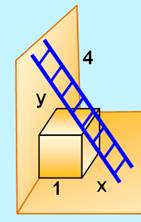
Énigme Une échelle de 4 m est appliquée à un mur. Elle s'appuie sur un cube
de 1m de côté. Quelles sont les longueurs x et y ? Solution Nous sommes exactement dans le cas étudié précédemment. L'échelle
représente le côté du carré inscrit et les valeurs sont: x = 0,362… et y
= 2,7609… |
Voir Brève
37-727 / Brève
37-727 /
Problème de
l'échelle & Problème de la double échelle (Ladder problems)
|
Celui dont les sommets sont les milieux du carré
d'origine est le plus petit. Cette page montre comment calculer les dimensions
lorsque le carré inscrit passe par un point de coordonnées x = y (petit carré
dans un coin du carré origine). Un calcul semblable permet de calculer les
dimensions dans le cas ou x est différent de y (Illustration). |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()