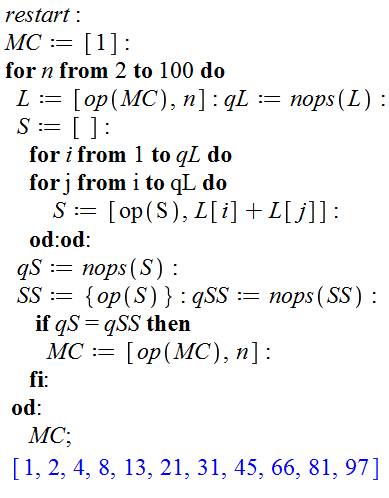Nombres de Mian-Chowla

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/09/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Général	Construction particulière					Glossaire Général
INDEX Nombres (Classification)	Ulam	Chanceux d'Ulam		Mian-Chowla	Sylvester
		Hofstadter–Conway		Suites équilibrées
			Sommaire De Cette Page >>> Caractéristiques >>> Liste >>> Somme >>> Programmation – Classique >>> Programmation – Expert

Suite de MIAN-CHOWLA – Caractéristiques
Famille	Nombre / Partition
Approche	Race de nombres qui se construisent en considérant les sommes inférieures à chacun d'eux. Nombres inventés par Abdul Majid Mian and Sarvadaman Chowla.
Définition	La suite des nombres de Mina-Chowla est définie par: a₁ = 1 a_n (n > 1) est le plus petit nombre, plus grand que a_n-1 , tel que les sommes (a_i + a_j) sont toutes distinctes pour tous i et j inférieur ou égal à n.
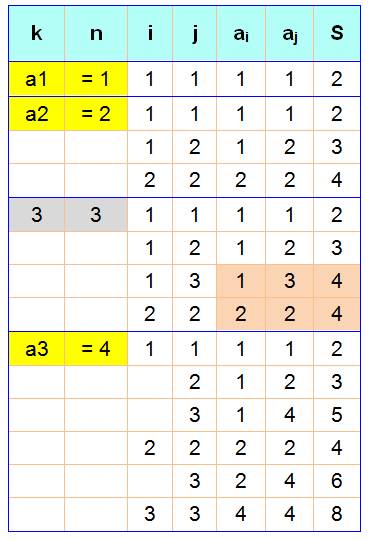
Exemples	En jaune les nombres retenus, les nombres de Mian-Chowla. Le cas 3 n'est pas retenu car la somme a_i + a_j est présente deux fois. Le 3 passe son tour et c'est le cas du 4 qui est examiné. Mais attention, les a_iet a_j sont ceux retenus (en jaune). Ne surtout pas reprendre les valeurs de i et j.
Anglais	The Mian–Chowla sequence is an integer sequence defined recursively in the following way. The sequence starts with: a₁ = 1. Then for n > 1 , a_n is the smallest integer such that the pairwise sum a_i + a_j is distinct, for all i and j less than or equal to n. Définition Wikipedia
Voir	Partition – découverte Partition – théorie Nombres chanceux d'Ulam Crible d'Ulam

Nombres de Mian-Chowla – Liste des 100 premiers

1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 290, 361, 401, 475, 565, 593, 662, 775, 822, 916, 970, 1016, 1159, 1312, 1395, 1523, 1572, 1821, 1896, 2029, 2254, 2379, 2510, 2780, 2925, 3155, 3354, 3591, 3797, 3998, 4297, 4433, 4779, 4851, 5123, 5243, 5298, 5751, 5998, 6374, 6801, 6925, 7460, 7547, 7789, 8220, 8503, 8730, 8942, 9882, 10200, 10587, 10898, 11289, 11614, 11876, 12034, 12931, 13394, 14047, 14534, 14901, 15166, 15688, 15972, 16619, 17355, 17932, 18845, 19071, 19631, 19670, 20722, 21948, 22526, 23291, 23564, 23881, 24596, 24768, 25631, 26037, 26255, …

Programmation – Classique

Initialisation (mise à zéro des mémoires).

Le premier nombre de Mian-Chowla (MC) est mis à 1.

Boucle d'examen des nombre de 2 à 100.

L est la liste des nombres MC, y compris provisoirement le nombre n en examen. qL donne la quantité d'éléments.

Ouverture d'une liste S où nous mémoriserons toutes les sommes possibles.

Double boucle en i et j pour calculer toutes les sommes et les placer en S. qS est la quantité de sommes réalisées.

SS est l'image de S mais en terme d'ensemble (tous les éléments en double sont éliminés).

S'il y a autant d'éléments dans la liste S que dans l'ensemble SS, c'est qu'il n'y a pas de doublon et la valeur de n peut être retenue. Elle est placée dans MC.

MC; est l'instruction qi demande l'impresion de MC

Programmation – Expert

Cette programmation très concise est due à Robert Israel (2014). Citée en OEIS A05282

Nécessite une connaissance avancée de Maple et une très bonne maitrise e de la logique.

Suite	Nombres chanceux d'Ulam Nombre chanceux d'Euler Nombre chanceux par plage
Voir	Crible d'Ératosthène
Site	Mian-Chowla Sequence – Wikipedia Mian-Chowla Sequence – Wolfram MathWorld OEIS A005282 – Mian-Chowla sequence
Cette page	http://villemin.gerard.free.fr/aNombre/TYPSEQUE/Mianchow.htm