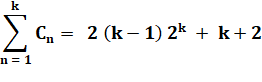|
|||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES de CULLEN
|
Anglais: Woodall numbers and Cullen Numbers
|
Famille |
Nombre / Diviseurs / Multiplicatif / Premiers |
|
Définitions |
NOMBRES PREMIERS DE CULLEN Nombre
premier de la forme Cn = n . 2n + 1 n est un nombre
entier supérieur à 0. |
|
Exemples |
3 = 1 x 21
+ 1 9 = 2 x 22
+ 1 25 = 3 x 23 + 1 |
|
Historique |
Introduit en 1905 par le père Cullen (1867-1933). Mentionné dans un livre de Guy. En 1976, Hooley montre qu'ils sont presque tous composés. |
|
Divisibilité |
W(p
+ 1)/2 ou W(3p – 1)/2 selon
que le symbole de Jacobi est égal à + 1 ou
à -1, respectivement. |
|
Premier |
C141
= 39305 0634124102 2328695670 3455542737 1542904833 = 0,39… 1045
Les suivants 1, 141,
4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, 481899,
1354828, 6328548, 6679881, …
393050634124102232869567034555427371542904833
|
|
|
|||
|
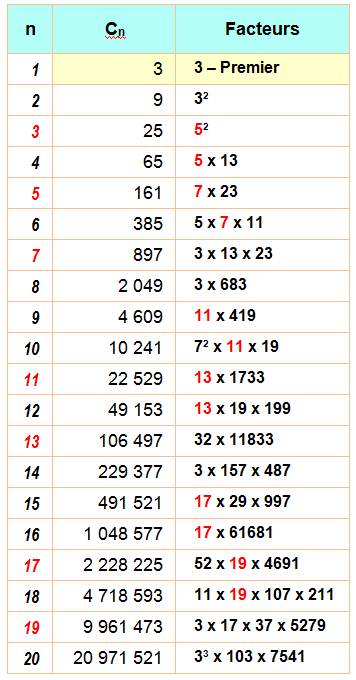
Les
vingt premiers Remarquez que les nombres en rouge sont premiers et
qu'ils se retrouvent dans les facteurs des deux nombres précédents. C'est une propriété générale. |
|
||
|
Les
16 premiers nombres PREMIERS de Cullen Cn pour n prenant les
valeurs indiquées => Ce sont les seize connus actuellement. Leur recherche a dû attendre l'arrivée des ordinateurs.
Le plus grand, découvert en 2009, compte plus de deux millions de chiffres. |
3, 141, 4713, 5795,
6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, 481899, 1354828,
6328548, 6679881, … ? |
||
|
Divisibilité |
Cp – 1
et Cp – 2 sont divisibles par
p. Ex: p = 5 alors: C3
= 25 et C4 = 65 Voir Nombres en rouge dans le tableau |
|
Premier |
C141
= 39305 0634124102 2328695670 3455542737 1542904833 = 0,39… 1045
393050634124102232869567034555427371542904833
|
|
Récurrence |
Cn = 4 (Cn–1 – Cn–2) + 1 Ex: C4 = 4 (C3 – C2) + 1 =
4(25 – 9) + 1 = 65 |
|
Somme |
Ex: C1 + C2
+ C2 + C4 = 2 x 3 x 24 + 4 + 2 = 102 = 3 +
9 + 25 + 65 = 102 |
|
|
||
|
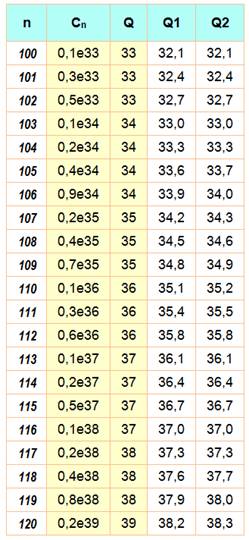
La
quantité de chiffres dans un nombre de Cullen peut être déterminée à un près
en prenant le logarithme du
nombre (on ignore le 1 final): Q2 = log10
(n . 2n + 1) Q1 = log10
(n) + n . log10(2) Le
tableau montre les valeurs de Cn pour n de 100 à 120, valeurs sous
la forme 0,3e33 qui veut dire 0,3 1033 soit (colonne 2), une
quantité de chiffres exactement égale à 33. Les deux colonnes de droites
indiques les valeurs trouvées en calculant les logarithmes (approchés pour Q1
et exacts pour Q2). Notez
qu'en prenant la valeur plafond
de Q1 ou Q2, on retrouve la quantité exacte. |
|
|
|
|
||
|
Liste
des unités des cent premiers nombres 3, 9, 5, 5, 1, 5,
7, 9, 9, 1, 9, 3, 7, 7, 1, 7, 5, 3, 3, 1, 3, 9, 5, 5, 1, 5,
7, 9, 9, 1, 9, 3, 7, 7, 1, 7, 5, 3, 3, 1, 3, 9, 5, 5, 1, 5,
7, 9, 9, 1, 9, 3, 7, 7, 1, 7, 5, 3, 3, 1, 3, 9, 5, 5, 1, 5,
7, 9, 9, 1, 9, 3, 7, 7, 1, 7, 5, 3, 3, 1, 3, 9, 5, 5, 1, 5,
7, 9, 9, 1, 9, 3, 7, 7, 1, 7, 5, 3, 3, 1 … Répétitives sur un
cycle de 20 Note que tous les
Cullen sont impairs (évidemment). |
||
|
Le cycle se répète sur les dizaines, les centaines,
etc. Précaution: ne pas compter les k premiers nombres pour
observer le cycle. |
C(U) = 20 C(DU) =
100 C(CDU) =
500 C(MCDU) =
2500 etc. C(k
chiffres) = 4 x 5k |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremCull.htm |
![]()