|
Édition du: 05/04/2023 |
|
INDEX |
Dénombrements - MOTIFS |
|||||
|
Nombres de
Catalan – Développements |
||||||
Faites
un double-clic pour un retour en haut de
page
![]()
|
NOMBRES DE CATALAN ESCALIER Combien de façons pour construire l'escalier ? |
||
|
|
Sommaire de cette page >>> Escaliers >>>
Pavage de l'escalier avec N rectangles |
Débutants Glossaire |
Anglais : Catalan Numbers
|
Combien de manières y a t'il de construire un escalier dans un
carré, les marches étant quelconques,
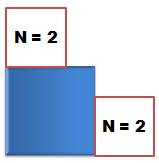
l'escalier ne dépasse pas la diagonale ? Carré de 2 x 2
2 possibilités Carré de 3 x 3
5 possibilités Carré de 4 x 4
14 possibilités Ce sont bien
évidemment les nombres e Catalan. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Chemins de Manhattan
/ Chemins de
Dyck
|
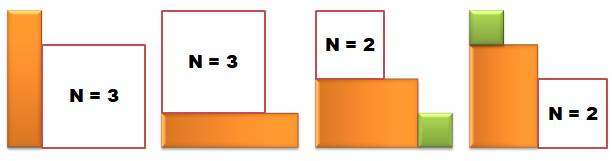
N = 2 Q = 2 |
Deux possibilités (Q = 2) avec deux rectangles (N = 2) de tailles
différentes. |
|
|
N = 3 Q = 5 |
Le grand vertical (3-1) deux fois comme N = 2; idem en horizontal. Plus un cas avec le carré (2+2). |
|
|
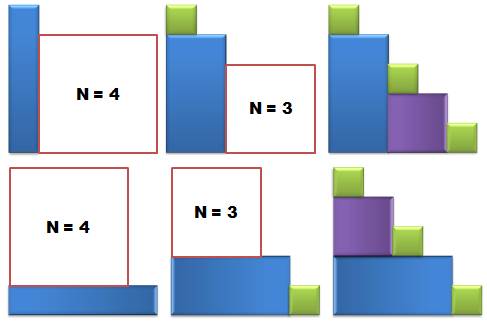
N = 4 Q = 5 + 5 + 2 + 2 = 14 |
Les carrés blancs indiquent que le motif se répète autant de fois que
pour N. Ex: remplacez la carré N = 3 cinq fois avec chacun des motifs de N = 3. |
|
|
N = 5 Q = 14 + 14 + 1 + 4 + 4 + 1 + 2 + 2 = 42 |
La suite du démombrement s'effectue
de la même façon en imaginant toutes les variétés de nouveaux grands rectangles
associés aux motfis de rangs inférieurs. |
|
![]()
|
Suite |
||
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/CataEsca.htm
|
|
![]()