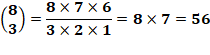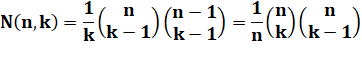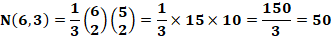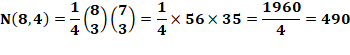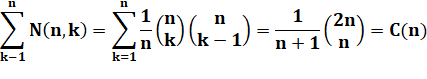|
Édition du: 06/01/2024 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres de NARAYANA Nombres qui se
présentent en triangle comme le triangle
Pascal. Nombreuses applications en combinatoire. Par exemple, pour le
comptage de la quantité de configurations de parenthèses. Nom donné
d'après Tadepalli Venkata Narayana (1930-1987), un mathématicien
indo-canadien. |
||
|
|
Sommaire de cette page >>> Triangle de Narayana ou triangle de Catalan >>> Exemple de dénombrement: parenthèses >>> Exemple de dénombrement: chemins >>> Propriétés des nombres de Narayana >>> Listes des nombres de Narayana |
Débutants Glossaire |
|
Nombres de Narayna Ils se présentent sous la forme d'un triangle
selon la valeur de n et de k Les applications sont nombreuses. Certaines ont
présentées en OEIS A001263. Par exemple: nombre de permutations qui évite {1,3, 2} et qui a k – 1 descentes;
nombre de chemins à travers n plaques de verre, entrant et sortant d'un côté,
de longueur 2n et avec k réflexions. |
Triangle de Narayana
Suite >>> |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Formule de calcul Ils sont exprimés en utilisant les coefficients
binomiaux. Rappel du calcul de ces
coefficients
|
Exemple
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Suite de
Narayana et super nombre d'or
|
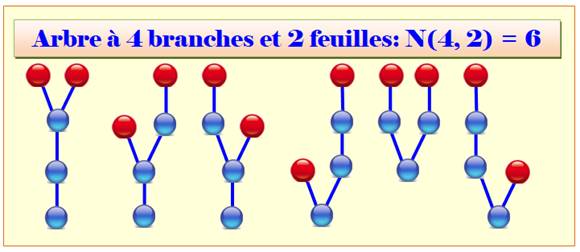
N(4,2) = 6 N(4,3) = 6 Quantité de configurations de 4 paires de parenthèses avec soit 2
paires internes (rouge) ou 3 paires. Pour être complet: configurations avec 1 seule paire et avec quatre
paires de parenthèses enfouies. |
2 paires internes
1 paire interne
|
3 paires internes
4 paires internes
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
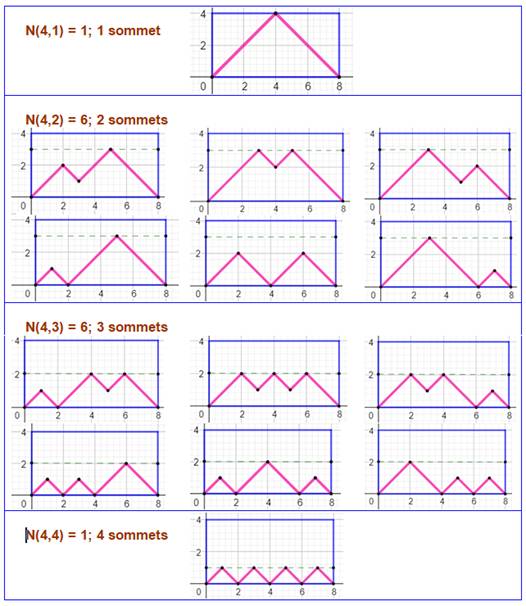
Il s'agit de la quantité de chemins de Dyck (Dyck
paths) comportant exactement k sommets. Plus précisément: quantité de chemins de coordonnées (0, 0) à (2n, 0)
comportant k sommets et, construits avec des mouvements de type nord-est (1,
1) et sud-est (1, -1) avec y ≥ 0. Ici, k = 4. |
|
|
Voir Chemins sur réseaux
|
Nombres de Catalan La somme des nombres de Narayana sur la nième ligne est égale au nième
nombre de Catalan. |
|
|
TABLES
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||