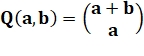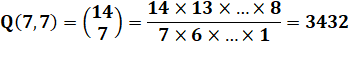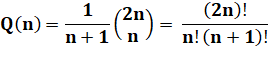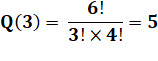|
Édition du: 28/03/2023 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
CHEMINS de MANHATTAN
Déplacement vers
la droite ou vers le haut seulement. Par nature, ces chemins sont
naturellement auto-évitants. C'est aussi la
manière dont se déplace la tour aux
échecs. En interdisant
les déplacements au dessus de la diagonale montante, on définit les nombres
de Dyck. |
||
|
|
Sommaire de cette page >>> Approche: déplacement de la tour >>> Déplacement de la tour – Dénombrement |
Débutants Glossaire |
Manhattan
|
À New York, dans le quartier de Manhattan, les rues se croisent à
angle droit. Le plan date de 1811, créant une matrice de rues presque
parfaite.
|
|
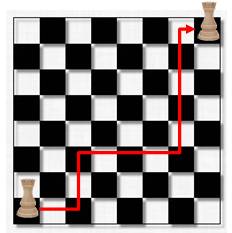
Mouvement de la tour aux échecs Dans ce cas, la tour
part du coin bas-gauche et doit rejoindre le coin haut-droit en se déplaçant
vers la droite ou vers le haut. Quelle est la quantité de chemins possibles sur
l'échiquier 8 × 8 ? Ce type de chemin est aussi qualifié de parcours
du taxi dans les rues à angle de droit de Manhattan
(New York). C'est aussi les façons de monter les marches d'un escalier en admettant des marches
de toute taille (staircase walk). |
Voir Échecs |
|
|
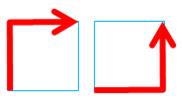
Sur une seule case (2 × 2
points) T(1) = 2 |
|
|
|
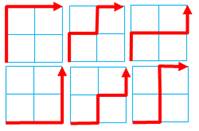
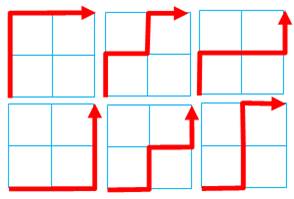
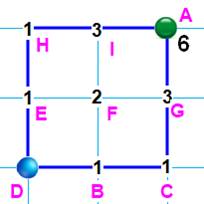
Sur une grille 3 × 3
points T(2) = 6 On compte (figure du bas) Chaque point représente le centre d'une case de
l'échiquier. Notez que: le côté mesure
deux unités, mais il y a trois points sur un côté. Pour aller du départ (D) à l'arrivée (A), il y a
6 chemins possibles:
|
|
|
|
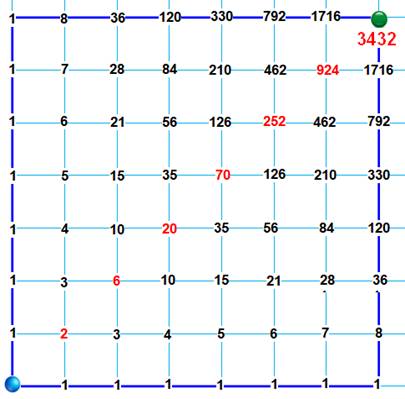
Échiquier complet 8 × 8 Chaque point est repéré par la quantité de
chemins possibles pour l'atteindre. C'est la somme des deux quantités en bas et sur
la gauche. Oui ! C'est bien le triangle
de Pascal selon la diagonale descendante (Voir en bas à gauche): 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 … |
|
|
|
Formule Quantité de chemin depuis l'origine pour
rejoindre le point de coordonnées (a, b): expression en coefficient
binomial. Notez que le point origine à pour coordonnées (0,
0) et le point en haut à droite (7, 7). |
Exemple pour le point A
(7,7)
|
|
|
Formule Ces nombres sont les nombres
de Catalan; calculé à partir du nombre central sur chaque ligne du triangle
de Pascal |
Exemple n = 3
|
|
Nombres de Catalan |
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,
742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420,
24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452,
18367353072152, 69533550916004, … OEIS A000108 |
|
Applications Exemples Richard Stanley en avait identifié 214. |
|
Haut de page (ou double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||