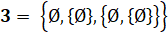NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/08/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des NOMBRES
Débutants Logique	ADDITIVE			Glossaire Arithmétique
INDEX Théorie des nombres Puissance Décomposition	Partition	Nombres et couleurs	Arithmétique de Peano
		Sommaire de cette page >>> Axiomatique de Peano >>> Arithmétique de Peano >>> Construction des nombres

Axiomatique de Peano

Arithmétique de Peano

Construction des nombres entiers

Comment en 1889, Guiseppe Peano construit une arithmétique à partir de l'ensemble vide et la notion de successeur.

L'axiomatique de Peano définit les nombres entiers naturels sans dire comment construire leur ensemble. La notion de cardinal le permet >>>

Anglais: Peano's axioms / Peano Arithmetic

Giuseppe Peano (1858-1932)

Mathématicien et linguiste italien.

Pionnier de l'approche formaliste des mathématiques.

Travaux exécutés en parallèle de ceux de Richard Dedekind (1831-1916).

Voir Courbe de Peano

Voir Contemporains

Axiomatique de Peano
Définitions	Dans l'arithmétique de Peano, on utilise: une constante: 0 une fonction unaire S qui désigne le successeur les fonctions binaires + et x. Les termes sont des éléments combinant symboles et fonctions, comme S(x) + S(y). Un énoncé désigne une propriété qui prendra son sens en fonction de la valeur des variables qu'il contient: vraie ou fausse, démontrée ou réfutée.
Les cinq axiomes définissant l'ensemble des entiers naturels	1. L'ensemble contient un élément particulier noté 0. 0 est donc un entier naturel. 2. À chaque élément n de l'ensemble correspond un successeur .noté: S(n) Tout entier naturel a possède un successeur. 3. L'élément particulier noté 0 n'a pas de prédécesseur. Seul 0 n'est le successeur d'aucun élément. 4. L'application est injective. Des nombres entiers distincts ont des successeurs distincts. 5. L'ensemble possède la propriété de récurrence. Si une propriété est vérifiée pour 0 et si, pour tout entier naturel n qui la vérifie, S(n) la vérifie également, alors la propriété est vraie pour tous les entiers naturels.
Axiomes de Peano (narratif)	Il existe un ensemble N avec: 1) ses éléments sont appelés les entiers naturels; 2) un élément 0 qui appartient à N appelé zéro; et 3) une application S de N dans N, dite application successeur, vérifiant les propriétés suivantes: 0 n'est le successeur d'aucun entier (l'application S ne produira jamais 0). deux nombres entiers qui ont même successeur sont égaux; l'application est injective. si une partie A de n contient 0 et elle est stable par S, alors A est égale à N. C'est l'axiome de récurrence. Stable veut dire que S(A) est inclus dans A.

Anglais

Écriture symbolique

Arithmétique de Peano
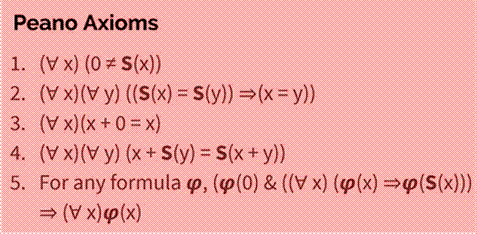
Axiomatisation de l'arithmétique de notions basiques aux concepts pointus		Objectif double: comme pour la théorie des ensembles, créer les fondements de l'arithmétique en définissant un langage logique qui va permettre de définir toutes les notions de l'arithmétique en prenant comme base cinq axiomes qui définissent les nombres entiers naturels; et disposant de ce cadre logique, permettre d'étudier les fonctions calculables, et, en conséquence, aller jusqu'à établir les théorèmes d’incomplétude de Gödel.
Construction de l'arithmétique Les cinq axiomes permettent de définir l'addition et la multiplication, puis toutes les propriétés classiques de l'arithmétique usuelle: commutativité, associativité, distributivité, etc.		Numération Le successeur de 0 est noté 1; celui de 1 est noté 2, etc. Addition Quelles que soient les valeurs de a et b, éléments de N: a + 0 = a a + S(b) = S(a + b) Multiplication Quelles soient les valeurs de a et b, éléments de N: a x 0 = 0 a x S(b) = a x b + a
Outils de la construction	Parmi les outils principaux, on trouve: la relation R (a, b, c …) entre n termes; les connecteurs logiques: conjonction, disjonction, implication, équivalence et négation; les quantificateurs: pour tout x et il existe x. le symbole d'égalité = (relation binaire)
Arithmétique élémentaire
Exemples de calcul	Rappels a + 0 = a (1) a + S(b) = S(a + b) (2) Exemples a + 1 = a + S(0) selon la définition du nombre 1. = S(a + 0) selon (2). = S(a) selon (1). a + 2 = a + S(1) selon la définition du nombre 2. = S(a + 1) selon (2). = S(S(a)) selon le résultat précédent. a + 3 = S(S(S(a))) …

Voir Opérations de l'arithmétique

Merci à Serge Paccalin

Construction des nombres – Méthode des ensembles dite de Von Neumann
Méthode La construction est conduite à partir de l'ensemble vide et, elle fait appel à la notion de cardinal (cad: de simple comptage des éléments).		Ensemble vide.
		Ensemble comprenant un unique élément, l'ensemble vide.
		Ensemble comprenant l'ensemble vide et l'ensemble comportant un élément, soit deux ensembles.
		Ensemble comprenant les ensembles 0, 1 et 2, soit trois ensembles.
Théorie	Point de départ: la théorie des ensembles et l'ensemble vide identifié à 0. On construit les entiers naturels de la façon suivante: L'ensemble vide est un entier naturel noté 0; Soit n un entier naturel, alors l'ensemble est aussi un entier naturel, appelé successeur (immédiat) de n. Tout entier naturel est construit à partir de ces deux règles. Exemples Successeur de 0: Successeur de 1: Successeur de 2: Pour assure l'existence d'un ensemble contenant tous les entiers naturels, il faut aussi introduire l'axiome de l'infini .

Zéro barré: unicode hexadécimal 00D8

Voir Système de numération unaire / Union (U) / John von Neumann

Merci à Philippe Caillaud pour ses remarques et corrections

Retour	Nombres et couleurs
Suite	Théorie des ensembles
Voir	Problème des quatre couleurs pour les cartes Actualités 2017 Théorie des nombres – Index
DicoNombre	Nombre 0 Nombre 1
Sites	Arithmétique de Peano – BibM@th.net Axiomes de Peano – Wikipédia Axiomes de Peano - Définition et Explications – Techno-Science Axiomatique des nombres – Christine Laurent-Thiébaut – 2014 – pdf 61 pages Axiomes et nombres – Gys M. Tuyman – pdf 300 pages Construction des entiers naturels – Wikipédia Entiers naturels et relatifs – Daniel Perrin Logique et théorie du calcul – Arithmétique de Peano Peano's Axioms – Wolfram MAthWorld
Cette page	http://villemin.gerard.free.fr/aMaths/ThNb/Peano.htm