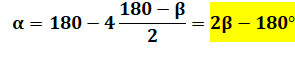Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 17/07/2023 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Rectangle et triangle
	Carré oblique	Carré et triangle équil.	Calculs d'angles
	Cercle et demi-cercle	Trois cercles tangents	Trois triangles réunis

CALCULS d'ANGLES par comparaisons progressives Passer d'un angle inconnu dans une figure à un autre angle connu par comparaisons, notamment en considérant que la somme des angles dans un triangle vaut 180°.
	Sommaire de cette page >>> Triangles isocèles >>> Triangle rectangle et triangles isocèles	Débutants Géométrie Glossaire Géométrie

Triangles isocèles		haut
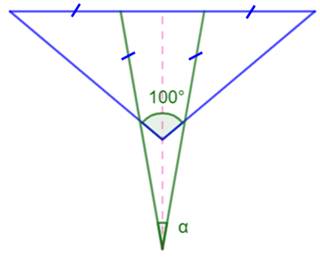
Construction Un triangle isocèle dont l'angle au sommet bêta vaut 100°. Sur chacun des sommets à la base, on dessine un triangle isocèle de même taille (marques d'égalité des côtés sur la figure). Les côté prolongés (verts) se coupent en formant un angle alpha. Quelle est la valeur de cet ange ? 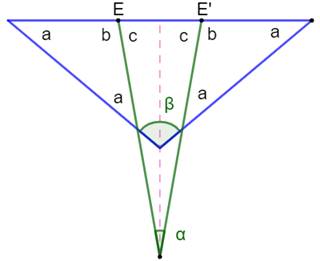Démonstration Avec comparaison des angles de proche en proche: Cas général Si l'angle de 100° est nommé bêta, la relation devient:	L'angle alpha est en relation constante avec l'angle bêta quelle que soit la position du point E.

Triangle rectangle et triangles isocèles		haut
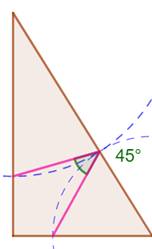
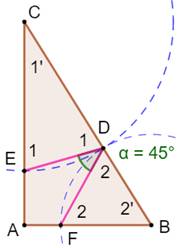
Construction Dans un triangle rectangle, on dessine deux triangles isocèles à partir des sommets comme indiqué (cercles pointillés montrant l'égalité des côtés). Démontrer que l'angle alpha vaut 45°, quelle que soit la taille du triangle rectangle. Démonstration Avec comparaison des angles:

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/Angles.htm