NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/01/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
Index général >>> INDEX	Index Divisibilité	A^n + B^n	Somme puissances (1/2)
	A² + B²	A^n – B^n	Somme puissances (2/2)
			Soustraction puissances
		Sommaire de cette page >>> Rappel & bilan >>> Exemples

Divisibilité

d'une somme de puissance (2/2)

Bilan et exemples numériques. Voir première partie >>>

Rappel et Bilan
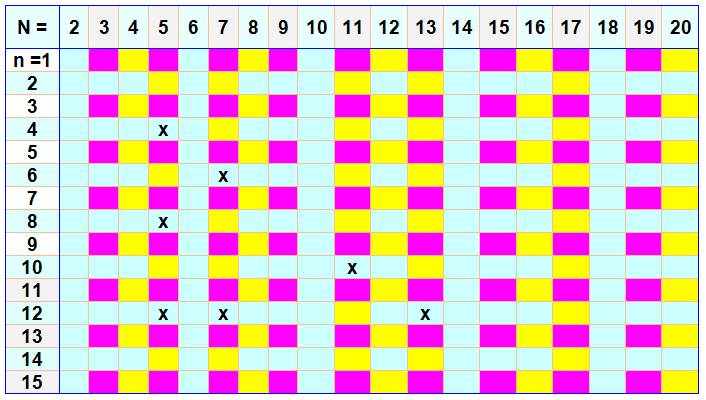
N est impair N | 1^n + 2^n + 3^n + ... + (N – 1)^n N divise cette somme sauf si N = 3 + 6k et n est pair ou N ≠ 3 + 6k et n = N - 1	N est pair N | 1^n + 2^n + 3^n + ... + (N – 1)^n N divise cette somme si N = 4 k et n est impair
Bilan Bleu N ne divise pas la somme en puissance n Jaune et Rose N divise la somme en puissance n Notez que la divisibilité est assurée pour tout N et n impairs (rose) La croix sert de repère pour les explications qui suivent.

Voir Somme des carrés de 1 à n

EXEMPLES
Pour N = 3 Sur le tableau précédent, la colonne N = 3 nous indique que N ne divise la somme S = 1^n + 2^n que pour n impair À droite, on donne successivement: n, S, S/3 valeur de l'exposant, valeur de la somme des puissances, et sa division par 3. Exemple avec N = 3, soit 2 termes: 7, 129, 43 => 1^7 + 2^7 = 1 + 128 = 129 et 129 / 3 = 43	1, 3, 1 2, 5, 5/3 3, 9, 3 4, 17, 17/3 5, 33, 11 6, 65, 65/3 7, 129, 43 8, 257, 257/3 9, 513, 171 10, 1025, 1025/3 11, 2049, 683 12, 4097, 4097/3 13, 8193, 2731 14, 16385, 16385/3 15, 32769, 10923 16, 65537, 65537/3 17, 131073, 43691 18, 262145, 262145/3 19, 524289, 174763 20, 1048577, 1048577/3
Pour N = 5 La colonne N = 5 nous indique que N divise la somme S = 1^n + 2^n + 3^n + 4^n dans tous les cas, sauf (cellule bleue avec petite croix) lorsque n est un multiple de 4 (en fait 5 – 1). n, S, S/5 valeur de l'exposant, valeur de la somme des puissances, et sa division par 5. Exemple avec N = 5, soit 4 termes: 7, 18700, 3740 => 1^7 + 2^7+ 3^7 + 4^7 = 1 + 128 + 2187 + 16384 = 18700 et 18700 / 5 = 3740	1, 10, 2 2, 30, 6 3, 100, 20 4, 354, 354/5 5, 1300, 260 6, 4890, 978 7, 18700, 3740 8, 72354, 72354/5 9, 282340, 56468 10, 1108650, 221730 11, 4373500, 874700 12, 17312754, 17312754/5 13, 68711380, 13742276 14, 273234810, 54646962 15, 1088123500, 217624700 16, 4338079554, 4338079554/5 17, 17309140420, 3461828084 18, 69107159370, 13821431874 19, 276040692700, 55208138540 20, 1102999460754, 1102999460754/5
Pour N = 7 La colonne N = 7 nous indique que N divise la somme S = 1^n + 2^n + 3^n + 4^n + 5^n + 6^n dans tous les cas Sauf (cellule bleue avec petite croix) lorsque n est un multiple de 6 (en fait 7-1) n, S, S/7 valeur de l'exposant, valeur de la somme des puissances, et sa division par 7. Exemple avec N = 7, soit 6 termes: 7, 376761, 53823 => 1^7 + 2^7+ … + 6^7 = 18700 + et 18700 / 5 = 3740 + 78125 + 279936 = 376761 et 376761 / 7 = 53823	1, 21, 3 2, 91, 13 3, 441, 63 4, 2275, 325 5, 12201, 1743 6, 67171, 67171/7 7, 376761, 53823 8, 2142595, 306085 9, 12313161, 1759023 10, 71340451, 10191493 11, 415998681, 59428383 12, 2438235715, 2438235715/7 13, 14350108521, 2050015503 14, 84740914531, 12105844933 15, 501790686201, 71684383743 16, 2978035877635, 425433696805 17, 17706908038281, 2529558291183 18, 105443761093411, 105443761093411/7 19, 628709267031321, 89815609575903 20, 3752628871164355, 536089838737765

Retour	Divisibilité des sommes de puissances (1/2)
Voir	Soustraction puissances A^n + B^N Divisibilité – Index Somme de puissances
Aussi	Diviseurs Nombres consécutifs Formes polynomiales divisibles Somme de cubes
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/SomPuis1.htm