|
|||||||||||||||||||||||||||||
![]()
|
DIVISEURS – FACTEURS Débutants La
division ouvre la porte sur la divisibilité. 12
est divisible par 4 car 3 x 4 = 12. Quels
sont tous les nombres qui en divisent un autre? 15
est divisible par 3 et aussi par 5. |
Voir Cours de 5e / Brève
de maths N°197
|
Multiples et diviseurs |
|
|
|
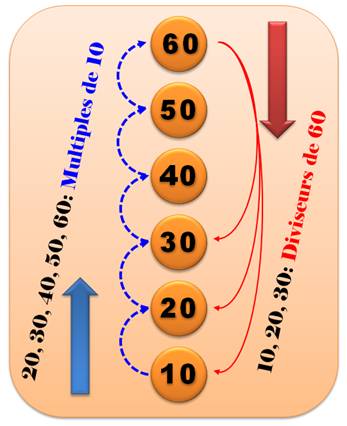
20, 30, 40, 50, 60,
etc.
60 On dit que 10 est un diviseur
de 60. On remarque que 20 et 30 sont aussi des diviseurs de
60. Ce n'est pas le cas des autres multiples: 40 et 50. 60 est multiple de 10 10 est diviseur de 60 |
|
|
|
|
||
|
|
À partir de 3, je crée ses multiples: 3 x 2 = 6 3x 3 = 9 3x 4 = 12 … 6, 9, 12 … sont les multiples
de 3. Choix: 111. Multiples de quels
nombres? 111 = 3 x 37 111 est multiple de 37 37 n'est le multiple d'aucun nombre. 111 est un nombre composé. 37 est un nombre premier. |
|
|
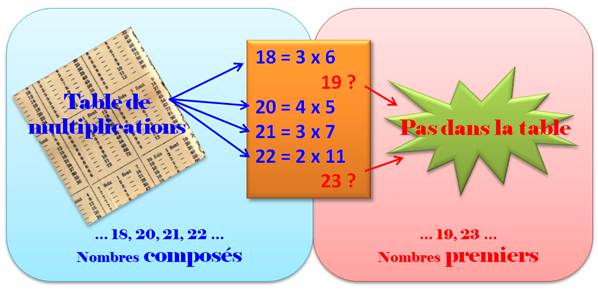
Illustration Les nombres figurant
dans les tables de multiplication se décomposent en produits: ce sont les nombres
composés. D'autres ne figurent dans aucune table de multiplication: ce sont
les nombres premiers. Exemple
de décomposition maximale pour atteindre le fond le plus bas
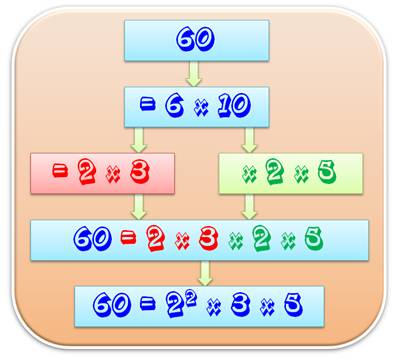
Le nombre 60 est de
manière évidente le produit des nombres 6 et 10. En reprenant chacun de ces
nouveaux nombres, il est possible de leur trouver un produit: 6 = 2 x 3 et 10
= 2 x 5. Par contre, impossible de trouver des produits pour 2, 3 et 5. Ils
sont tous trois têtes de liste ou premiers.
Et 60 et un nombre composé du produit de 2
par 2 par 3 et par 5, ou en bref: 60 = 2² x3 x 5. |
||
|
|
||
|
|
12 est divisible par 3. Il est composé. 17 n'est pas divisible, sauf par 1 et par 17. Il est premier. |
|
|
|
60 est divisible par 20 qui est divisible lui-même par 10. 20 est un diviseur composé 60 est aussi divisible par 5 qui n'est pas divisible. 5 est un diviseur premier |
|
|
Parmi eux seuls trois sont des diviseurs premiers (ou
facteurs). Et, avec ces trois seuls premiers, il est possible de
définir le nombre 60.
|
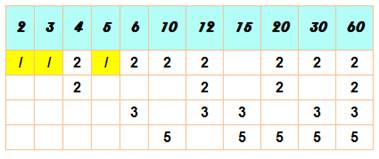
60 est divisible par: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. 60 possède douze diviseurs. Pour chaque diviseur, on essaie de les mettre sous la forme d'un
produit: Exemple: 12 = 2 x 2 x 3
Trois nombres résistent: 2, 3 et 5 ce sont des nombres premiers. Les autres diviseurs
sont des nombres composés à partir de ces trois là. Et 60 lui-même n'échappe pas à cette propriété: 60 = 2 x 2 x 3 x
5 |
|
Bilan
|
Nous
connaissons bien les multiples et les diviseurs. Un
nombre qui n'a pas de diviseurs est premier, sinon il est composé. Parmi
tous les diviseurs d'un nombre certains sont des nombres premiers, les
diviseurs premiers ou facteurs. Ceux-ci sont les briques suffisantes pour
construire tous les nombres. Cette
propriété est le théorème fondamental de l'arithmétique. |
|
Les types de nombres selon
facteurs et diviseurs |
|
|
|
|
60 = 2² x 3 x 5 61 = 61 62 = 2 x 31 63 = 3² x 7 64 = 26 65 = 5 x 13 |
|
|
|
60 est un nombre dont le facteur le plus grand
vaut 5 61 est premier. 62 et 65, avec deux facteurs non répétés sont
semi-premiers. 63 et 60 sont des nombres avec carrés. 64 est une puissance parfaite. |
|
|
|
La somme des diviseurs de 60 vaut 168 ou 108 en
lui retirant 60. Ce nombre est supérieur à 60. Le nombre 60 est dit abondant. Pour 61, la somme est 61 + 1 = 62 et en lui
retirant 61, il reste 1 qui est nettement inférieur à 61; Ce nombre 61, comme
tous les nombres premiers est particulièrement déficient. Le cas de 6 est intéressant. Les diviseurs de 6
sont: 1, 2, 3, sans le 6 et la somme est égale à 1 + 2 + 3 = 6. Cette somme
est égale au nombre. Le nombre 6 fait partie de la famille des nombres
parfaits. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
|
![]()