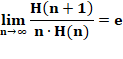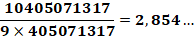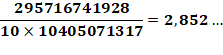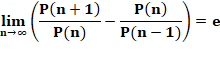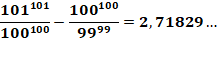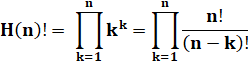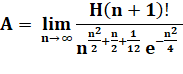|
Édition du: 18/09/2022 |
|
INDEX |
FACTORIELLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres hypertriangulaires et
nombres hyperfactorielles Nombres
construits à partir des nombres triangulaires et des nombres factoriels en
élevant chacun des termes à la puissance du même nombre.
|
||
|
|
Sommaire de cette page >>> Hypertriangulaires – Sommes >>> Quatre types de nombres >>> Hypertriangulaires – Puissances >>> Hyperfactorielles >>> Récapitulatif numérique jusqu'à 1000 |
Débutants Glossaire |
|
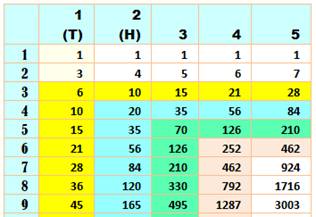
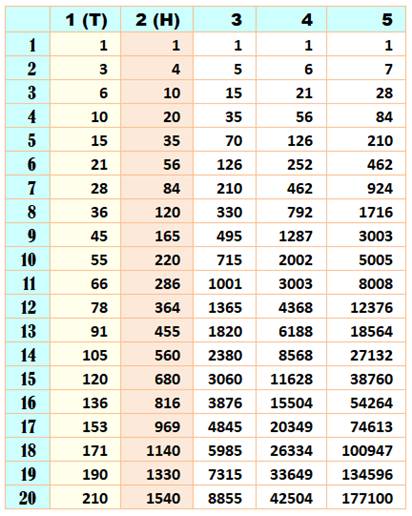
Somme multi-cumulée des factorielles classiques.
Chaque nombre de la table est égal la somme de son voisin du dessus avec son
voisin de gauche. La table donne la valeur de ces nombres pour les
indices de 1 à 20 et pour les ordres de 1 à 5. L'ordre 1 correspond aux nombres triangulaires
classiques (T). L'ordre 2 correspond aux nombres tétraédriques
(H), somme cumulée des trinagulaires. Remarquez la symétrie de la table par rapport à
la diagonale principale:
|
|
|
Somme ou produit des nombres
successifs avec ou non leur puissance

Voir Brève
918
|
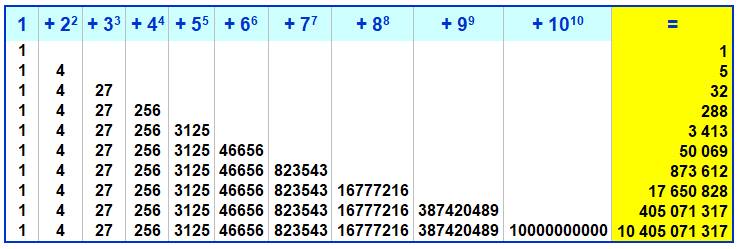
Ces nombres sont souvent appelés hypertriangulaires. Chacun est la somme de tous les nombres jusqu'à lui
et porté à leur propre puissance. HT3 = 11 + 22 + 33 = 32 |
Aucune formule ne permet le calcul direct de ces
nombres. Tout au plus peut-on encadrer la valeur. Toutefois ces nombres peuvent être exprimés comme
le produit de discriminants de certains
polynômes. Voir lien in fine. |
||
|
Table des premiers nombres
hypertriangulaires (en jaune)
Voir Table –Suite Liste des valeurs des nombres
hypertriangulaires 0, 1, 5, 32, 288, 3413, 50069, 873612, 17650828, 405071317,
10405071317, 295716741928, 9211817190184, 312086923782437, 11424093749340453,
449317984130199828, 18896062057839751444, 846136323944176515621, …. OEIS A001953 Cas des hypertriangulaires-plus 1: Cas des hypertriangulaires-moins 1:
|
|||
|
Propriété de la suite Le rapport entre
deux valeurs successives de la suite, divisé par n tend vers e.
La converge vers
e est très lente. Au dixième rang l'écart avec e =
2,718… est encore de 0,123… |
Exemples
|
||
|
Propriété des puissances Cette relation avec les rapports des puissances des
nombres est nettement plus convergente.
|
Exemple
|
||
|
Ces nombres se calculent comme les factorielles,
mais en portant chaque nombre à sa puissance. H3! = 11 × 22 × 33 = 108 |
Cas du 0 Hn! = nn × H(n-1)! H1! = 1 × H(0)! |
||
|
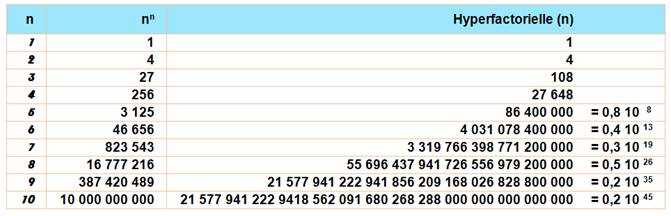
Valeurs pour n de 1 à 10
Liste des valeurs des
hyperfactorielles 1, 1, 4, 108, 27648, 86400000, 4031078400000,
3319766398771200000, 55696437941726556979200000,
21577941222941856209168026828800000, 215779412229418562091680268288000000000000000,
61564384586635053951550731889313964883968000000000000000 |
|||
|
Curiosité Avec l'hyperfactorielle 5, on atteint le nombre
de millisecondes
dans un jour. Le tableau montre comment les produit se
combinent pour donner: 24 × 60 × 60 × 1000 = 86 400
000. |
Calcul particulier de
l'hyperfactorielle 5.
The fifth hyperfactorial: 5⁵ × 4⁴ × 3³ ×
2² × 1¹ = 86 400 000 milliseconds is exactly 1 day. |
||
|
Formulations |
|
||
|
Calcul Pas de formule permettant un calcul direct, mais
une formule d'approximation asymptotique. |
Les hyperfactorielles ont été étudiées à partir
du 19e siècle par Hermann Kinkelin et James Whitbread Lee
Glaisher. Kinkelin: tout comme les factorielles peuvent
être interpolées en continu par la fonction gamma, les hyperfactorielles
peuvent être interpolées en continu par la fonction K. Glaisher:
formule asymptotique pour les hyperfactorielles, analogue à la formule
de Stirling pour les factorielles. |
|
|
Fonction K |
La fonction K est une généralisation de
l'hyperfactorielle aux nombres
complexes, similaire à la généralisation de la factorielle à la fonction
gamma. |
|
|
Constante de Glaisher-Kinkelin Cette constante
fait intervenir l'hyperfactorielle Cette formule fait penser à la formule
de Stirling, la constante A jouant le rôle de |
A = 1,28242712910062263687...
|
|
Récapitulatif numérique jusqu'à 1000
|
Les
52 nombres triangulaires,
hypertriangulaires, factoriels et hyperfactoriels jusqu'à 1000: 1, 2, 3,
4, 5, 6, 10, 15, 21, 24, 28, 32, 36, 45, 55, 66, 78, 91, 105, 108, 120, 136,
153, 171, 190, 210, 231, 253, 276, 288, 300, 325, 351, 378, 406, 435, 465,
496, 528, 561, 595, 630, 666, 703, 720, 741, 780, 820, 861, 903, 946, 990. Liste
de ces nombres selon
leur type: [1,
F], [1, hF],
[1, hT], [1,
T],
[2, F], [3,
T], [4, hF],
[5, hT], [6, F], [6, T], [10, T],
[15, T], [21, T],
[24, F], [28, T],
[32, hT], [36, T],
[45, T], [55, T],
[66, T], [78, T],
[91, T], [105, T],
[108, hF],
[120, F], [120, T], [136, T],
[153, T], [171, T],
[190, T], [210, T],
[231, T], [253, T],
[276, T], [288, hT], [300, T],
[325, T], [351, T],
[378, T], [406, T],
[435, T], [465, T],
[496, T], [528, T],
[561, T], [595, T],
[630, T], [666, T],
[703, T], [720, F],
[741, T], [780, T],
[820, T], [861, T],
[903, T], [946, T],
[990, T] Les nombres
108 et 288 sont
les plus grands hyper inférieurs à 1000. |
Accès à ces nombres dans le DicoNombre
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |