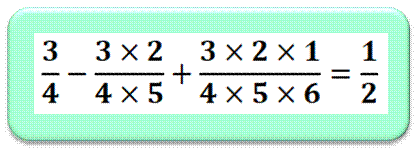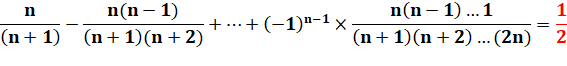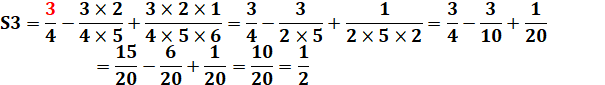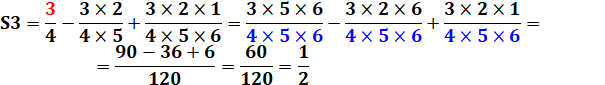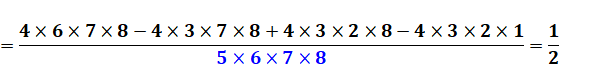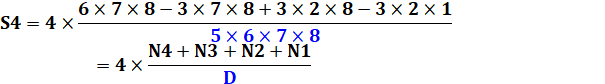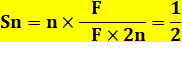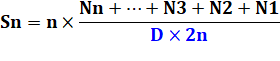NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/08/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	COMPTER - Combinatoire
Débutants Dénombrement	FACTORIELLES				Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Introduction		Tronquées	Généralisées
		Alternée	Tables des tronquées		Sous-factorielle
		Somme = 1/2	Nombres de Stirling
		Sommaire de cette page >>> Approche numérique >>> Factorisation avec n = 4 >>> Démonstration

FACTORIELLES TRONQUÉES

Somme alternée égale à 1/2

Exemple

Généralisation

Approche numérique
Méthode Avant d'aborder la formule littérale, voyons ce qui se passe avec quelques valeurs de n. Deux calculs sont présentés: avec simplification des fractions dès que possible, et avec mise sous dénominateur commun dès le départ. Cette dernière méthode de calcul est plus propice au passage à la forme littérale.
Exemples
Méthode avec simplifications immédiates Méthode avec mise sous dénominateur commun

Factorisation avec n = 4

Reprenons le calcul avec n = 4. Le nombre 4 est mis en facteur commun.

Adoptons ces notations pour montrer que le numérateur se factorise:

On effectue successivement les sommes du numérateur, de droite à gauche (les deux colonnes de droite sont destinées à la vérification des calculs):

Calcul numérique

Calcul avec factorisation

Cette dernière présentation montre comment nous avons transformé une somme en produit, lequel produit se retrouve au dénominateur et se simplifie intégralement.

Généralisation

On montre facilement, mais laborieusement, que cette identité se reproduit pour tout n.

Démonstration - Principe
L'écriture sous forme littérale est fastidieuse. La démonstration suit exactement la trame développée pour n = 4. On pose: Avec: Etc. On calcule: Etc.

Voir Formalisation complète et autres preuves sur le site: Sum of series – a finite alternating series

of ratios of factorial-like numbers equals ½ - Several proofs – Graeme McRae.

Retour	Factorielles tronquées Somme et produit
Suite	Somme et produit de 3 nombres consécutifs Division des factorielles tronquées Factorielle tronquée = carré? Factorielles généralisées Produit de k nombres consécutifs – Divisibilité
Voir	Coefficient du binôme Factorielles divisées Loto Partition en nombres consécutifs Programmation du calcul des factorielles Théorie des nombres – Index
DicoNombre	Nombre 1/2
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/Factdemi.htm