Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 16/10/2023 M'écrire Brèves de Maths

INDEX Triangles Géométrie Puissances	Théorème de Pythagore
	Débutants	Nomenclature – Types de démonstrations		Applications
	En quatrième	Approche	Calcul Aires	Dissections
	Toute figure	Historiques	Similitudes	Hypoténuse
	Triplets de P.	Chinoise (Chou Pei)	Algébrique	Pyramide
	Pappus-Clairaut

Théorème de Pythagore Spécial élève de quatrième Page d'approche du théorème de Pythagore et du secret des nombres à virgule.
Classe de 4^e	Sommaire de cette page >>> Découverte des nombres sans fin >>> Preuve muette du théorème de Pythagore >>> Recherche de la racine carrée	Débutants Géométrie Glossaire Géométrie

Voir aussi Le diaporama de Clément (9 ans) / Toutes les pages débutants

Découverte des nombres sans fin		haut
Pythagore et sa communauté Pythagore de Samos vivait vers les années 500 av. J.-C. Samos est une île grecque proche de la Turquie. Pythagore et les membres de son école avait une grande passion pour les nombres allant jusqu'à croire à leurs vertus magiques (mystiques).	Les nombres servent à compter: 1, 2, 3, … Mais ce sont aussi des symboles: 1 pour la raison 2 pour la féminité 3 pour la masculinité 4 pour la justice 5 pour le mariage (car 5 = 2 + 3) etc.
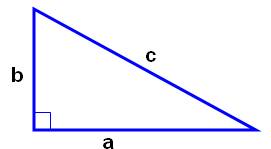
Théorème de Pythagore Cette communauté de mathématiciens redécouvre cette fameuse propriété des triangles rectangles. Elle était déjà connue des Babyloniens bien avant Pythagore. La postérité lui a tout de même donné le nom de théorème de Pythagore.	a² + b² = c²
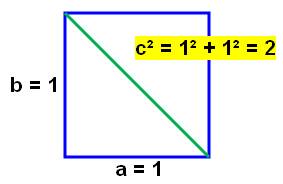
Le secret Parmi les membres, Hippase de Métaponte se met à calculer la longueur de la diagonale d'un carré en appliquant le théorème. Le carré de l'hypoténuse vaut: c² = 1² + 1² = 2. Mais que vaut c, le nombre qui multiplié par lui-même donne 2. On sait que pour 4, c'est 2 car 2 x 2 = 4. Hippase est déconcerté: il découvre que le nombre n'est pas un nombre classique et qu'il se situe entre 1 et 2 (on le nomme aujourd'hui "racine de 2" et ce nombre vaut: 1,4142… Symbole ). Pour lui et ses collègues, ce n'est pas pensable. Car pour eux, les nombres servent à compter les objets. Ce sont toujours des nombres entiers comme 1, 2, 10, 50, etc. Voilà qu'ils découvrent des nombres suivis de morceaux de nombres, des nombres à virgule. Une hérésie !	La longueur de la diagonale du carré ne tombe pas juste
La noyade Toute cette communauté, choquée, décide de taire ce terrible secret. Hippase ne tient pas sa langue. Il sera exclut de la communauté des pythagoriciens. Même, certains rapportent qu'il se serait jeté dans la mer pour se punir, ou qu'il fut jeté à la mer par ses condisciples.	Aujourd'hui on connait: les nombres entiers: 1, 2, 3, … les nombres fractions comme 1/2 = 0,5 ou comme 1/3 = 0,333… et les nombres sans fin comme

Voir Types de nombres – Débutants

Preuve muette du théorème de Pythagore		haut
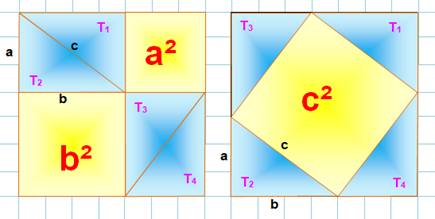
Voyez comment on transforme la figure de gauche en celle de droite. On y voit quatre triangles rectangles égaux que l'on fait glisser pour obtenir la figure de droite. On a alors l'égalité des aires: a² + b² + 4T = 4T + c² Et, en retirant les 4T, on a: a² + b² = c².

Voir Théorème de Pythagore avec d'autres figures que le carré

Recherche de la racine carrée		haut
On cherche de plus en plus de chiffres derrière la virgule. Pour cela, on commence par 1 puis 2 … En calculant le carré, on s'arrête dès que ce carré dépasse 2 (jaune). Alors, on ajoute un chiffre et on recommence. Exercice amusant à faire sur tableur.

Suite	Théorème de Pythagore – Débutant Théorème de Pythagore – Développements Théorème de Thalès – Débutant Théorème de Pythagore – Types de démonstrations Pages débutants – Index
Voir	Addition – Glossaire Années Pythagore Années Pythagore Décade de Pythagore Décade de Pythagore Nombres carrés Nombres polygones Nombres triangles Pythagore – Biographie Somme de carrés
Sites	Voir liste des liens
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPyth4e.htm