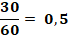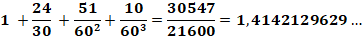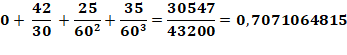|
Édition du: 19/09/2023 |
|
INDEX |
Théorème de Pythagore |
|||
![]()
|
Démonstrations historiques du Théorème de Pythagore Revue des
nombreuses démonstrations de ce célèbre théorème dit de Pythagore. Cette
page présente certaines démonstrations dues çà des hommes célèbres (on en
trouvera d'autres pages). Toutes les
démonstrations connues ont été recensées en 1940 (2e édition) par Elisha Loomis
(1852-1940). Henry Dudeney (1857-1930) a publié de nombreuses dissections (puzzles ou casse-têtes). |
||
|
|
Sommaire de cette page >>> Antiquité >>> Démonstration de Liu Hui >>> Démonstration d'Euclide >>> Démonstration de Léonard de Vinci >>> Démonstration telle que présentée en 1634 |
Débutants Glossaire |
Voir Types de démonstrations
du théorème de Pythagore
|
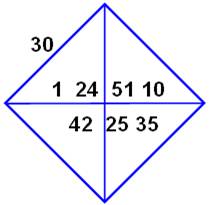
Babylone
(vers -1700) Ce dessin mésopotamien
représente le relevé des nombres cunéiformes figurant sur une tablette. Ils sont exprimés
par des fractions en base 60.
Une très bonne
approximation de racine
de 2. |
|
|
|
Chine
(entre – 1000 et 200) Les
Chinois connaissaient les propriétés du triangle rectangle vers -1100
(Tschou-Gun). Ce dessin chinois
représente une preuve très ancienne figurant dans le Zhoubi Saunjing. L'aire du carré oblique vaut la moitié de 4
fois les rectangles 3x4 plus une unité: 2 x 24 + 1 = 25; et, côté de ce carré
vaut: 5. Inde
(entre – 800 et – 600) Ce théorème a
été aussi mentionné dans les Baudhayana Sulba-sutra. Dans les deux
cas la relation du théorème n'est pas exprimée explicitement, mais les
indications s'y ramènent. Voir Démonstration
de Chou Pei Suan Ching / Brève 53-1058 |
|
|
|
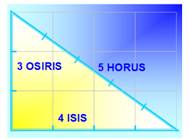
Égypte
(avant – 600) Ils connaissaient
les propriétés du triangle rectangle et les triplets associés. Le triangle
isiaque (3, 4, 5), sacré pour les prêtres égyptiens. Les triplets pour
les arpenteurs: ils mesuraient 6 pieds, 8 pieds sur les côtes du triangle
et s'arrangeant pour avoir 10 pieds sur le troisième côté. |
|
|
|
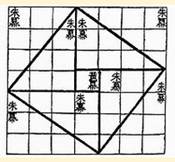
Pythagore
(vers – 580 à – 495) Pythagore et
son école sont sans doute les premiers à avoir démontré ce théorème qui
porte. La raison est à chercher dans le fait que cette école considérait
toute mesure commensurable à l'unité. Les figures ne comportant que des nombres entiers ont sans
doute été propices au raisonnement. Pythagore
connaissait le triangle
isiaque (3, 4, 5), utilisé quatre fois sur cette figure pour démonter le
théorème. Lui et son école avaient mis en évidence les triplets dits de Pythagore. Ils
auraient démontré ce théorème vers -
540. Cependant de nombreux chercheurs réfutent l'idée que Pythagore en soit
l'auteur. En tout cas, nous ne connaissons pas la démonstration de Pythagore. |
|
|
|
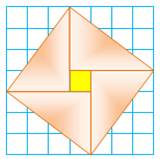
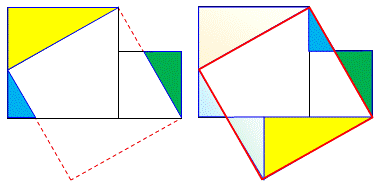
Démonstration par dissection. Puzzle de Gouzu par Liu Hui Puzzle reconstitué d'après les commentaires de Liu Hui dans le livre: Jiuzhang suanshu (Les Neuf Chapitres sur
l'art mathématique – 206 av.–220 apr. J.-C.) et le Zhoubi Suanjing Instructions Liu Hui donne des couleurs aux triangles et indique ceux qui doivent
sortir (découpe) et se placer (doigt) pour former le grand carré oblique. Notez que les trois déplacements à effectuer, se réalise par une
translation en diagonale. |
Interprétation d'après Liu Hui
Puzzle en deux étapes
|
|
|
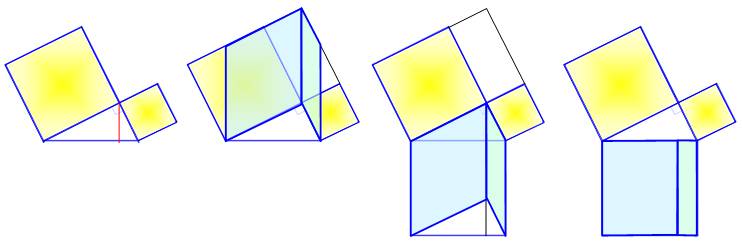
Démonstration express par transitivité des aires |
1) Le triangle rectangle initial et deux carrés sur les côtés. 2) Les deux parallélogrammes ont même aire que les carrés. 3) En les faisant glisser, ils se plaquent sur le triangle initial. 4) Ces parallélogrammes ont la même aire que les rectangles dont la
somme des aires est celle du grand carré.
|
|
|
|
||
Démonstration détaillée
|
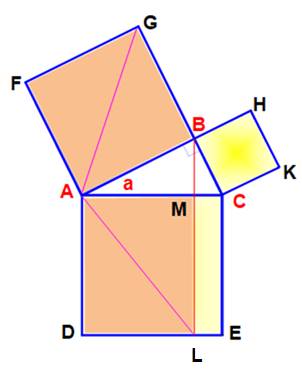
Proposition 47 du livre I (I, 47) des Éléments d'Euclide (vers -300). Construction Triangle rectangle ABC. Les carrés construits sur les côtés. La perpendiculaire BL. Démonstration Deux couples de triangles colorés qui ont la même
aire car même base et sommet sur une parallèle à la base: |
|
|
Les deux triangles colorés AFC et ABD sont égaux (isométriques): · du fait des carrés: AC = AD. · Angles en A Effectivement avec un angle et deux côtés égaux les deux triangles
dont isométriques. |
|
|
On reprend nos égalités: Par transition: Par addition: Même raisonnement avec la partie droite qui conduit à l'égalité des
surfaces jaunes Addition: Aire du petit carré + aire du
moyen carré |
|
|
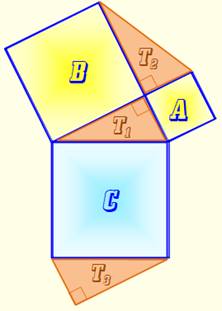
Construction Un triangle rectangle T1. Carrés notés A, B et C le long des côtés du triangle T1. Le triangle T2 est obtenu par rotation de 180° de T1
autour du sommet de l'angle droit. Le triangle T3 est construit sur un côté du carré C; il est
identique à T1. C'est possible car ils ont une longueur
d'hypoténuse commune. |
|
||||
|
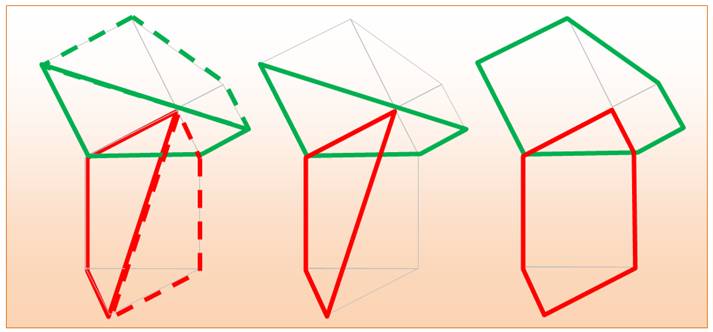
Principe de la démonstration (en termes d'aires)
|
|||||
|
VERT = VERT pointillé ROUGE = ROUGE pointillé |
VERT = ROUGE |
VERT = ROUGE |
|||
|
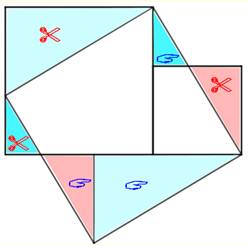
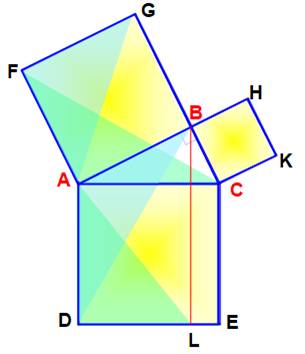
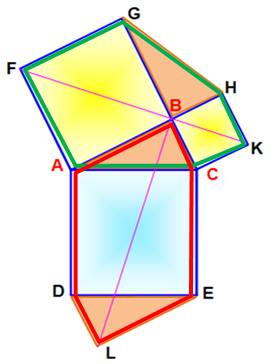
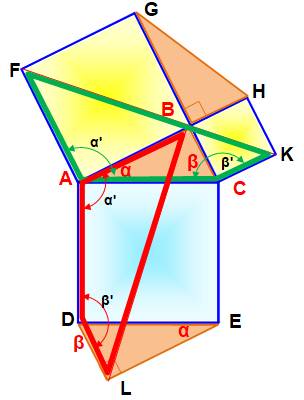
Alignement (figure du haut) On construit le segment FK qui partage les deux carrés jaunes en deux
parties égales le long de leur diagonale. C'est un axe de symétrie. Les deux triangles T1 et T2 sont isométriques;
alors, le point B se trouve sur l'axe de symétrie; les points F, B et K sont
colinéaires. Deux hexagones partagés en deux parties égales · Dans le cas VERT: chaque moitié contient les
moitiés des deux carrés jaunes et un triangle identique de chaque côté. · Dans le cas ROUGE: les deux triangles sont
partagés de la même manière; ainsi que le carré bleu. Symétrie axiale de
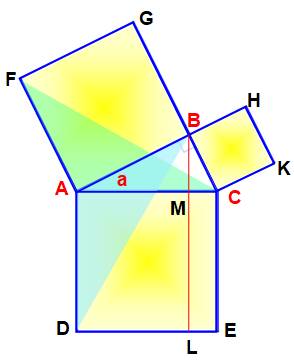
centre le milieu de BL. Comparaison VERT et ROUGE (figure du bas) Quadrilatère ACKF (vert) et ADLB (rouge). Effectivement: Les deux quadrilatères (vert et rouge) ont deux angles respectivement
égaux situés entre trois côtés respectivement égaux, ils sont isométriques. Comparaison des deux hexagones En doublant chacun des quadrilatères, on obtient deux hexagones isométriques: ACKHGF et
ADLECB. Chacun contient deux triangles T. En retirant ces deux triangles en
haut, il reste les deux carrés jaunes et en retirant deux triangles en bas,
il reste le carré bleu. Conclusion: aire des deux carrés jaunes
= aire du carré bleu. |
|
||||
Merci à
Michaël Aupetit pour ses remarques
Démonstration telle que présentée en 1634

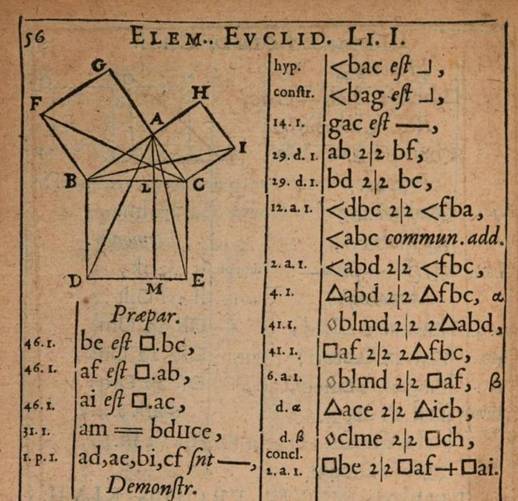
Cours
mathématique demonstré d'une nouvelle, briefve et claire méthode
De Pierre Hérigone (Mathématicien) –
1634
![]()
|
Retour |
·
Démonstrations du théorème – Dissections |
|
Suite |
|
|
Voir |
·
Triangles – Index |
|
Sites |
· Quelles démonstrations
pour le théorème de Pythagore ? – Alain Bernard et Brigitte Roussel |
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/DemoHi.htm
|