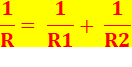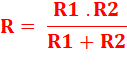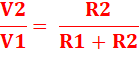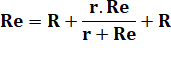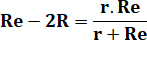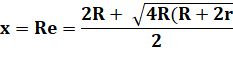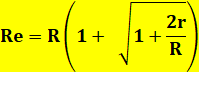|
|||||||||||||||||||||||||||||||||
![]()
|
Montage de résistances Utilisation
des résistances pour obtenir les tensions désirées. Comment
se comporte des résistances en enfilade (en série)
ou côte-à-côte (en parallèle)? |
|
|
|||||
|
|
Le courant est un
mouvement d'ensemble des électrons parmi leur mouvements propres
très erratiques (brownien) et d'autant plus désordonnées
que la température est élevée. Lorsque plusieurs
résistances sont présentes dans un circuit, on cherche à
trouver quelle serait la valeur de l'unique résistance qui les
représenterait. C'est la résistance
équivalente. |
||||
|
|
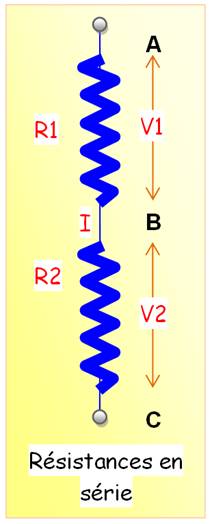
Exemple I = 1 A R1 = 10 V1 = 10 x 1 = 10
V V2 = 5 x 1 = 5 V V = 10 + 5 = 15 V |
||||
|
|
||
|
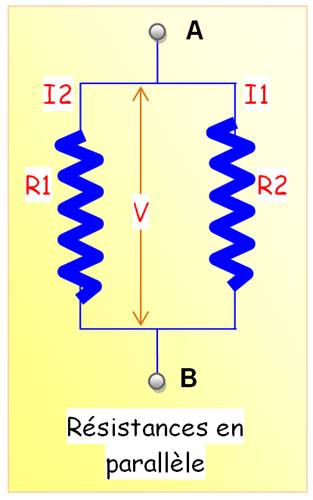
I = I1 + I2
V = R1 . I1 V = R2 . I2
V = R . I V = R (V/R1 + V/R2)
|
Exemples R1 = 10 R = 100 / 20 = 5 R1 = 10 R = 50 / 15 =
3,33 |
|
Voir Moyenne harmonique
|
Si les deux résistances sont de même valeur, alors
|
|
|
||
|
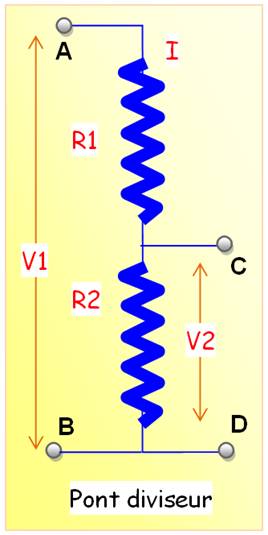
V1 = (R1 + R2) . I V2 = R2 . I
|
Exemples R1 = 10 V2 = 10/20 V1 = 1/2 V1 R1 = 10 V2 = 5/15 V1 = 1/3 V1 |
|
|
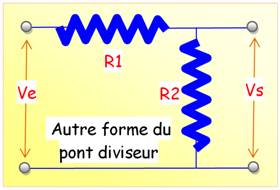
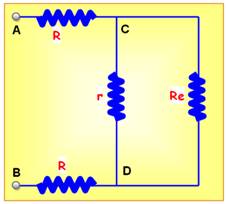
Autre forme du circuit
|
Voir La forme en biais |
|
|
|
||
|
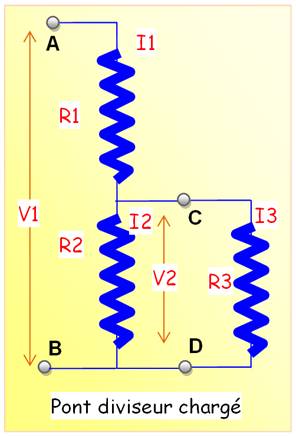
I1 = I2 + I3
|
Exemples R1 = 10 V2 =10x10/(10x20+10x10) = 100/300 = 1/3 de V1 R1 = 5 V2 =10x15/(5x150+10x15) = 150/900 = 1/6 de V1 |
|
|
|
||
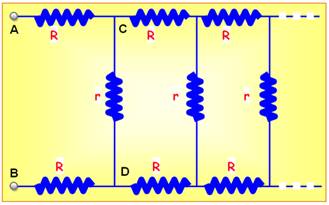
|
|
|
|
|
|
(Re
– 2R) (r + Re) = r . Re Re.r
+Re² – 2R.r – 2R.Re = r.Re Re²–
2Re.R – 2R.r = 0 |
|
|
|
x² – 2xR – 2R.r = 0 4R² + 8R.r = 4R (R + 2r) Oui
|
|
|
|
|
|
|
Le cas de R = 4 et r = 5 est
intéressant: Re = 4 + 4 = 4 + 4 x 3/2 = 4 + 6 = 10 |
|
|
Code de couleur des
résistances
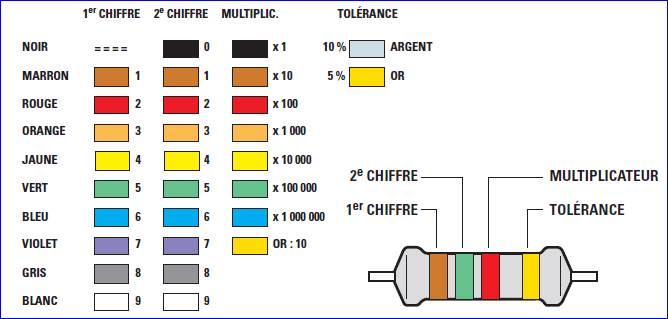
Source: Apprendre l'électronique en partant de
zéro.
Voir Nombre 1 et les suivants
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Electron/Resistan.htm
|
![]()