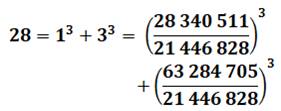Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	20	21		22	23		24	25	26	27	28	29

Nombre 28

Maths générales du 28

Maths détaillées du 28

Vingt-huit

Twenty-eight

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1100
Bases	446 2213
Romain	XX VIII Plus petit avec 6 chiffres

Suite

Nombre réversible (Strobogrammatique)

Caractérisation du nombre

Ami avec tous les parfaits

Composé

Congruent

Coster

Cunningham

Dihédral

Dissécable

Docile (amenable)

Extravagant

Grandville (ou S-parfait)

Harmonique

Heureux

Idonéal

Keith

Leyland en x^y – y^x

Narcissique de Keith

Ore (2^e)

Padovan

Pair

Palin10 (2 + 8 = 10)

Parfait

Pratique

Ramsey (3,8)

Semi-parfait primitif

Stirling 1 et 2

Ulam

Zumkeller

Triangulaire (7^e)

Pascal

Hexagonal (4^e)

Ennéagonal centré (3^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Chiffres et numération

28 + (2 × 8) = 44	Devient repdigit en ajoutant le produit de ses chiffres.
28 = 6+1+4+6+5+6 28^4 = 614 656	Narcissique de Keith Somme des chiffres de sa puissance 4.
28, 1144, 11224, 112222 2+8 = 1+1+4+4 = 1+1+2+2+4 = 1+1+2+2+2+2 & 2x8 = 1x1x4x4 = 1x1x2x2x4 = 1x1x2x2x2x2	Somme de chiffres et produits identiques. Plus petit motif, 4 fois.

Addition et soustraction

p(28) = 3 718	Quantité de partitions du nombre.
28 = 5 + 23 = 11 + 17 = 2 + 3 + 23 = 2 + 7 + 19 = 3 + 5 + 7 + 13 = 2 + 3 + 5 + 7 + 11	Le nombre 28 est le plus petit ayant, au moins, une partition à 2, 3, 4 et 5 termes distincts.
28 = M3 (M3 + 1) / 2 28 = 1 + 2 + 4 + 7 + 14 = 2² (2^3 - 1) = 1^3 + 3^3	Nombre parfait formé avec le nombre de Mersenne M3 = 2^3 – 1 = 7 Forme des parfaits. Propriété des parfaits. Seul parfait de la forme x^n + y^n avec n > 1. Nombre à moyenne harmonique entière.
28 = 2 + 3 + 5 + 7 + 11 208 = 2² + 3² + 5² + 7² + 11²	Somme des cinq premiers nombres premiers consécutifs. Coquetterie avec les carrés (28 et 208).
28 = 1 + 2 + 3 + … + 7	Partition unique avec sept chiffres différents. Nombre triangulaire: le 7^e Énigme: on a compté 28 poignées de mains dans cette réunion. Combien de personnes ? Solution: le premier touche n-2 mains; le suivant n – 3, etc. Total n (n – 1) / 2) = 28 n² – n = 56 => n = 8.
	Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 2 parmi 8.
28 = 1 + 2 + 3 + … + 7 = 14 + 15 – 1	Propriété utilisées dans une énigme de pesée avec 15 poids.
28 = 1 + 5 + 9 + 13	Nombre hexagonal: le 4^e
2, 8, 10, 18, 28	Nombre de Keith. Deux chiffres => on effectue la somme sur les deux nombres précédents. Nombre de Keith s'il se trouve dans la séquence ainsi produite.
1 = 1/2 + 1/4 + 1/7 + 1/14 + 1/28	Somme des inverses des diviseurs de 28. Nombre en division harmonique.
28 = (7+1) + (7–1) + (7x1) + (7/1)	Somme des quatre opérations.

Multiplication, division, diviseurs

28-Harshad = [112, 140, 224, 252, 280, 308, 336, 364, 392, 448, 476, 588]		Ces douze nombres sont 28-Harshad. Quotient 28 lorsque divisés par la somme de leurs chiffres. Rare.
		Factorielle triple de 2 = (3x0+1) (3x1+1) (3x2+1) = 1 x 4 x 7
28 = 10! / 360² = 3 628 800 / 129 600		Factorielle divisée.
	La somme des diviseurs du totient de n est égale à n. Liste: 1, 3, 15, 28, 255, 744, 2418, 20440, … OEIS A018784

Avec les puissances

28 = 1² + 1² + 1² + 5² = 1² + 3² + 3² + 3² = 2² + 2² + 2² + 4² = 1^3 + 3^3	Toutes les sommes de puissances de 2 à 5 avec deux à cinq termes (sans doublons du 1). Somme des deux premiers impairs au cube.
28 = 8² – 6²	Différence de deux carrés.
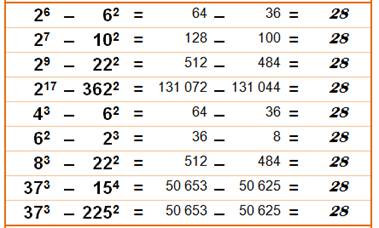
28 = 4^3 – 6² = 64 – 36 = 8^3 – 22² = 512 – 484 = 37^3 – 225² = 50 653 – 50 625	Seuls cas d'équation de Bachet pour k = 28. Différence entre un cube et un carré.
28 = 2^5 – 2^2	Différence de puissances d'un même nombre.
		Sommes de deux cubes rationnels.
		Différence entre puissances.

En puissance

784 (28² = 30² – 120 + 4) 29² = 841 (29² = 30² – 60 + 1)	Motif qui favorise la mémorisation de ces carrés.
19^3 = 6 859 & 6 + 8 + 5 + 9 = 28 28^3 = 21 952 & 2 + 1 + 9 + 5 + 2 = 19	Curiosité réciproque avec des cubes.
28^4 = 28^3 + 84^3	Bicarré somme de deux cubes.
	Curiosité avec la racine quatrième. Voir entrée ci-dessous
28^4 = 614 656 & 6+1+4+6+5+6 = 28 28^5 = 17 210 368 & 1+7+…6+8 = 28	Nombre NESCHIP. Double.

Dénombrement, jeux et curiosités

		Jeu du quatre 4.
28	Quantité de pavages uniformes convexes dans ℝ^3.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 0, 0] 3, [1, 0, 0, 1] 4, [1, 3, 0] 5, [1, 0, 3] 6, [4, 4] 7, [4, 0] 8, [3, 4]	9, [3, 1] 10, [2, 8] 11, [2, 6] 12, [2, 4] 13, [2, 2] 14, [2, 0]	15, [1, 13] 16, [1, 12] 17, [1, 11] 18, [1, 10] 19, [1, 9] 20, [1, 8]	6, [4, 4] 13, [2, 2] 27, [1, 1]

Voir Bases / Brésiliens

Voir	Voir le menu en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/Nb28Nb.htm