|
Édition du: 04/07/2021 |
|
INDEX |
TRIANGLES Éléments remarquables |
||
|
Éléments remarquables – Index |
|||
![]()
|
Éléments remarquables du triangle Triangle EXTOUCHE & Point de NAGEL Triangle
dont les sommets sont les centres des
cercles exinscrits. Propriétés des droites issues de ces trois points. Christian
Henrich von Nagel
(1803-1882): géomètre allemand. |
||
|
|
Sommaire de cette page >>>
Triangle de Nagel >>>
Point de Nagel >>>
Anglais |
Débutants Glossaire |
Nadel et Gergonne
|
Le point de Nagel et le point Gergonne
sont les points de concours de deux faisceaux de trois céviennes
remarquables. Ces droites relient les sommets du triangle
d'origine aux points de tangence:
Ces deux points sont des conjugués isotomiques (symétrie de construction via les milieux
des côtés). They both
involve cevians drawn from a vertex to the points of tangency of circles. |
|
– Extouch
triangle or Nagel triangle |
||
|
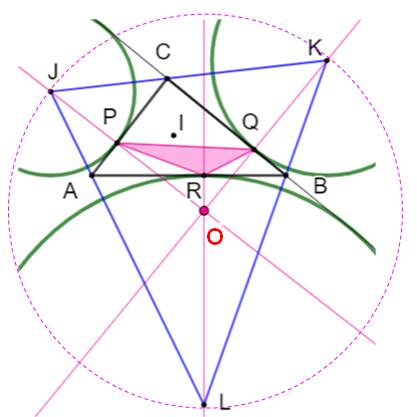
Construction Le triangle
ABC. Les centres J, K et L des cercles exinscrits Les points P, Q et R de tangence des cercles
exinscrits avec les côtés du triangle ABC. Point O: centre du cercle circonscrit. Point I:
centre du cercle inscrit. . Propriétés Le triangle PQR est le triangle de Nagel de ABC. |
|
|
|
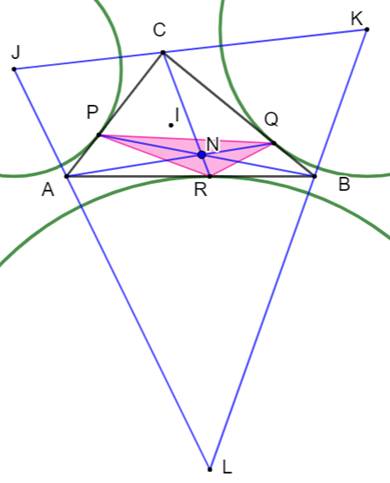
Construction Le triangle
ABC. Le triangle extouche PQR. Les droites AQ, BP et CR. Propriétés Les trois droites se coupent en un point unique,
le point de Nagel. Point X(8) de la nomenclature de Kimberling. Le point de Nagel est le centre du cercle inscrit
dans le triangle
médian. Le cercle circonscrit au triangle de Nagel est le cercle de
Mandart. Les segments AQ, BP et CR partagent le périmètre
du triangle ABC en deux parties égales. Ce sont les droites de partage du
triangle (triangle's splitters). |
|
||
|
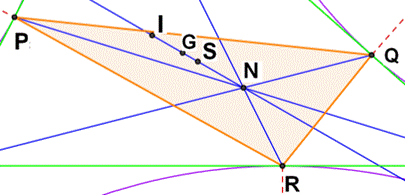
Alignement Les points suivants sont alignés sur la droite de
Nagel:
Relation:
IN = 3 IG |
|
||
|
Coordonnées du point de Nagel |
Trilinéaires: b + c – a
: c + a – b : a + b – c Barycentriques: a (b +
c – a) : b (c + a – b) : c (a + b – c) 1 + cos A : 1
+ cos B : 1 + cos C |
||
|
Construction
simple du point de Nagel X(8) |
||
|
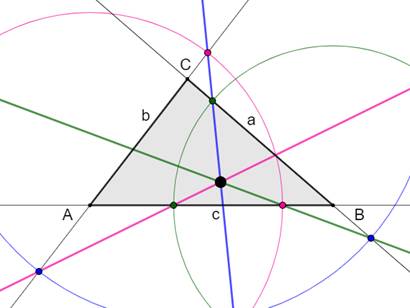
Construction Le triangle
ABC. Cercle (A, a) Rouge Cercle (B, b) Vert Cercle (C, c) Bleu Deux intersections pour chaque cercle avec les
côté de l'angle A, B ou C respectivement. Trois droites reliant ces intersections deux à
deux. Point de rencontre commun = point de Nagel. |
Construction du point de Nagel
|
|
|
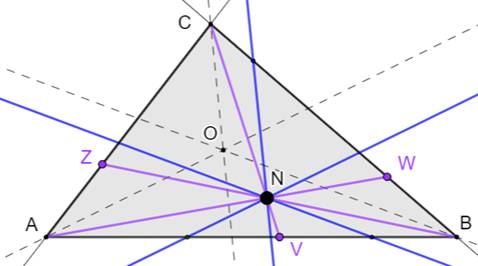
Comparaison Sur cette figure: En bleu les droite de construction du centre de
Nagel (cf. ci-dessus). En violet, les droites de définition du centre de
Nagel: du sommet au point de tangence du cercle exinscrit. En pointillés, les bissectrices des angles
internes du triangle. Elles sont parallèles aux droites de construction
(bleues). |
Comparaison
|
|
|
Given a triangle ABC, let TA,TB and TC
be the extouch points in which the A-excircle meets line BC, the B-excircle meets
line CA, and C-excircle meets line AB respectively. The lines ATA,
BTB, CTC concur in the Nagel point NG of
triangle ABC. The Nagel point is named after
Christian Heinrich von Nagel, a nineteenth-century German mathematician, who
wrote about it in 1836. The Nagel point is sometimes also called the bisected
perimeter point, and the segments ATA, BTB, CTC
are called the triangle's splitters. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triang
le/Remarqua/Nagel.htm |