|
Édition du: 03/07/2021 |
|
INDEX |
TRIANGLES Éléments remarquables |
||
|
Éléments remarquables – Index |
|||
![]()
|
Éléments remarquables du triangle Triangle EXINSCRIT & MITTENPUNKT Triangle
dont les sommets sont les centres des
cercles exinscrits. Propriétés des droites issues de ces trois points. |
||
|
|
Sommaire de cette page >>>
Triangle exinscrit >>>
Mittelpunkt >>>
Anglais et allemand |
Débutants Glossaire |
|
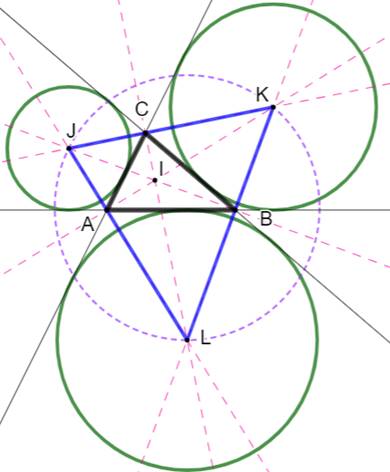
Construction Le triangle
ABC. Les côtés sont prolongés Les bissectrices
des angles internes et externes (pointillés). Les trois cercles exinscrits
dont les centres (j, K, L) sont les points des concours externes des
bissectrices. Le point de concours interne (I) est le centre du cercle inscrit. Définition Le triangle JKL est le triangle
exinscrit (Anglais: excentral triangle) Le cercle circonscrit à ce triangle (pointillés)
est le cercle de Bevan . Propriétés Le point I est l'orthocentre
du triangle JKL. Le triangle ABC est le triangle pédal
du triangle JKL. |
|
||
|
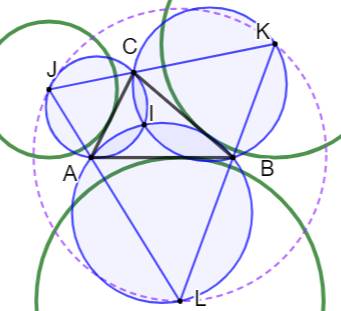
Le cercle passant par deux sommets du triangle
initial et le centre du cercle inscrit passe aussi par un centre de cercle
exinscrit (trois cercles bleus). Mesures du triangle exinscrit
Avec R = rayon du cercle circonscrit:
|
|
||
|
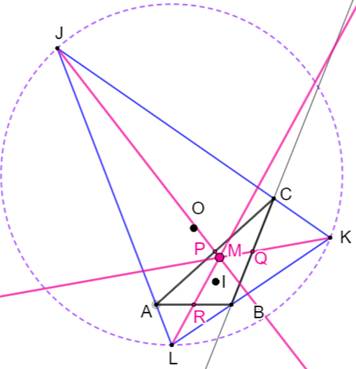
Construction Le triangle
ABC et son triangle exinscrit JKL Les points milieux des côtés P, Q et R. Les demi-droites JP, KQ et LR. Propriétés Ces trois droites se coupent en un point unique
le Mittelpunkt (ou middlespoint). C'est le point symédiane
du triangle exinscrit JKL. Point X(9) de la nomenclature de Kimberling. Ce point, le centre de gravité et le point de Gergonne
sont alignés avec GeG = 2 GM |
|
||
|
Coordonnées |
Trilinéaires: b + c – a
: c + a – b : a + b – c Barycentriques: a (b +
c – a) : b (c + a – b) : c (a + b – c) 1 + cos A : 1
+ cos B : 1 + cos C |
||
|
The mittenpunkt (also called the middlespoint) of a triangle ABC is
the symmedian point of the excentral triangle, i.e., the point of concurrence
M of the lines from the excenters Ji through the corresponding
triangle side midpoints Mi. |
Allemand: MITTEL
|
Mittelpunkt: centre,
point central, point de convergence Kultureller Mittelpunkt: centre culturel. Cœur (anatomie): das Herz. Angle au centre: der Mittelpunktswinkel. Centre du cercle inscrit: der Mittelpunkt des
Inkreises. Centre du cercle circonscrit: der Mittelpunkt des Umkreises. Médiane: die Mittellinie oder die Schwerlinie. Médiatrice: die Mittelsenkrechte (Senkrechte: verticale ou perpendiculaire) Moyenne: die Mittelwert |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triang
le/Remarqua/Mittenpu.htm |