NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/11/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	CERCLE / DISQUE
Débutants Géométrie	Rectangle dans le cercle				Glossaire Géométrie
INDEX Cercle Géométrie	Général		Abaques	Méthode graphique
	Un quadrant		Deux quadrants	Quatre quadrants
	Lycée	Sommaire de cette page >>> Exemple pratique >>> Méthode graphique >>> Calcul aire gauche >>> Bilan

RECTANGLE et CERCLE

Deux quadrants

Nous poursuivons le calcul de l'aire de l'intersection d'un rectangle de grande dimension avec un disque. Le rectangle empiète sur deux quadrants.

Exemple pratique
Calcul de l'aire () de la partie jaune: intersection du rectangle avec le disque. Exemple numérique avec un cercle de rayon 8 unités et le coin B du rectangle en coordonnées (4, 3). Notez que AB horizontal n'est pas un cas particulier. Dans d'autres situations similaires, il suffit de faire tourner le cercle pour se retrouver dans ce cas.

Méthode graphique (ordre de grandeur)
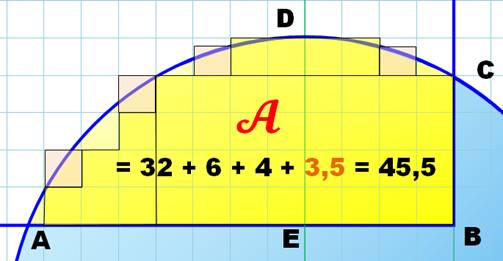
Faites le dessin sur un quadrillage aussi fin que vous le souhaitez et comptez les carreaux couverts par l'intersection. En jaune, les carrés élémentaires évidents En rose, une estimation des parties en frontière. Nous verrons que cette estimation n'est pas si loin de la réalité. Et même, cette valeur va servir de repère pour vérifier la validité de nos calculs.	Le comptage des petits carrés donne une aire voisine de 45,5 carreaux alors que le calcul produit:45,45 carreaux.

Découpage de la figure

La méthode de calcul géométrique va consister à découper la figure en deux grandes parties:

A_G à gauche (AED) avec DE sur un rayon du cercle; et

A_D à droite (BCDE), toujours en profitant de DE sur le rayon.

Calcul de l'aire AG
La partie gauche AG est composée d'un segment de cercle A1 et d'un triangle rectangle A2. On calcule: l'aire du triangle rectangle puis la valeur de h qui permettra le calcul de l'aire du segment. Nous suivrons les valeurs numériques au fur et à mesure pour conforter nos calculs. Pythagore est toujours à l'œuvre!
Dans le triangle OAE	AE² = OA² - OE² = R² – y²
Aire A2		A2 = 18,540…
Dans le triangle AED	AD² = AE² + ED² = (R² – y²) + (R – y)² = 2R (R – y)	AD = 8,944…
Dans le triangle OAH	h² = OH² = OA² – AH² = R² – AD²/4	h = 6,633…
Aire du segment A1		A1 = 8,299…

Calcul de l'aire AD
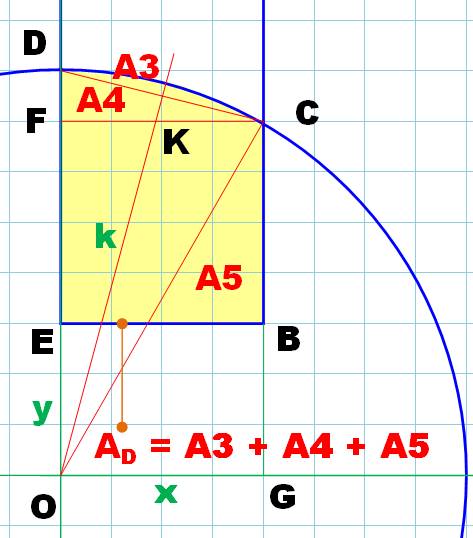
La partie droite AD est composée d'un segment de cercle A3, d'un triangle rectangle A4 et d'un carré A5 . On calcule: L'aire du carré, l'aire du triangle rectangle puis la valeur de k qui permettra le calcul de l'aire du segment.
Dans le triangle OFC	OF² = OC² - FC² = R² - x²	OF = 6,928…
Aire carré A5		A5 = 15,713…
Valeur de DF		DF = 1,071…
Aire triangle 4		A4 = 2,143…
Dans le triangle CDF	DC² = DF² + FC² = DF² + x²	DC = 4,141…
Dans le triangle ODK	k² = R² - DC² / 4	k = 7,727…
Aire segment 3		A3 = 0,755…
Aire totale	A = A1 + A2 + A3 + A4 + A5	A = 45,452…

Pour le fun, formule complète

Aire complète (A)

Application numérique en conservant les radicaux

Valeur de A

45,452055222629329029…

Voir Abaque

Bilan

La formulation fait peur! N'est-ce pas? Un logiciel de calcul est le bienvenu. Malheureusement, il reste un cas à voir qui va s'avérer un peu plus retors.

Retour	Rectangle et cercle – Un quadrant
Suite	Rectangle et cercle – Quatre quadrants
Voir	Angles Bissectrices Cercle – Index Cône Géométrie – Vocabulaire Lunule Secteur de disque Sphère Trigonométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Rectang2.htm