|
|||||||||||||||||||||||||||||||||||
![]()
|
À
TROIS autour d'une TABLE RONDE Combien de possibilités pour
disposer les convives. Le cas à trois constitue une
initiation. Nous en profitons pour inclure
une énigme qui traite des proximités à table. Il existe de nombreux
problèmes de disposition de personnes autour d'une table quelle soit linéaire
(comme un grand banc), ou rectangulaire (avec des personnes de chaque côté)
ou bien encore ronde. Le dénombrement des
possibilités d'arrangements devient vite compliqué. À la main dans les cas où le nombre de
personnes est faibles (1 à 5); avec ordinateurs pour des cas de 6 à 10 ou 12
personnes); et avec la théorie |
En résumé
|
Quantité
de dispositions avec k convives (k personnes):
|
|
|
||
|
Table en
ligne (banc ou table en U)
3
! se lit factorielle 3. |
N = 3 ! = 6 Voici les 6
arrangements ABC BAC CAB ACB BCA CBA |
|
|
Table en
rond
|
N = 2 Voici les
2 arrangements ABC ACB Notez
que dans le cas de la table ronde: ABC, BCA et CAB
sont identiques quant au voisinage des convives. Peu importe que A (par exemple)
soit à l'une ou l'autre des trois places. |
|
|
|
||
|
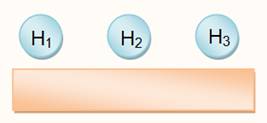
Table en
ligne
|
H1 H2 H3 OUI H1 H3 H2 Non H2 H1 H3 Non etc. N = 1 |
|
|
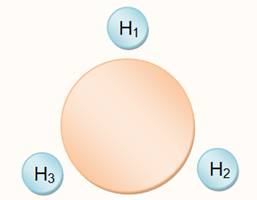
Table en
rond
|
H1 H2 H3 H4 OUI H124
H324 H¹ 1234 NON N = 1 |
|
|
S'en
persuader!
|
Toutes les
permutations [1, 2, 3], [1,
3, 2], [2, 1, 3], [2,
3, 1],
[3, 1, 2], [3, 2, 1] Permutations sans
voisinage avec distance unité [1, 2, 3] |
|
|
|
||
|
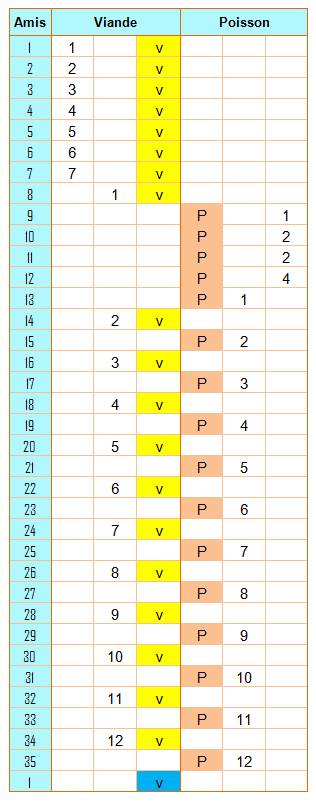
Problème
|
Solution Il a quatre types de situations selon qui est à droite:
Les P – P sont intercalés dans une chaine P – P – P (ou plus de P) car
tout V intermédiaire est déjà compté. Les P – V sont aussi nombreux que les V – P. Ces ¾ sont égaux à 12:
3p/4 = 12 soit p = 16. Total des amis: 19 + 16 = 35. On vérifie que le dernier (P) boucle bien sur le premier (V). C'est un
des ¾ de P – V. |
|
|
Illustration
|
|
|
D'après: La bosse des maths – La Dépêche – 26/03/2014
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()