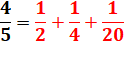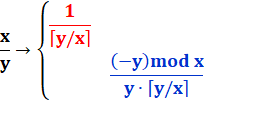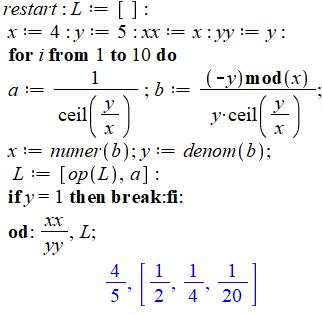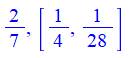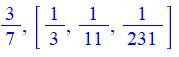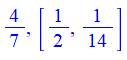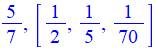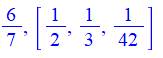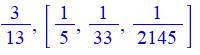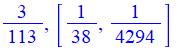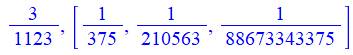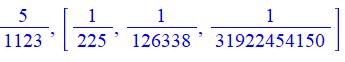|
Édition du: 03/11/2023 |
Faites un double-clic pour un retour en haut de page
![]()
|
Fractions égyptiennes par l'algorithme glouton Algorithme glouton pour le calcul des fractions égyptiennes. Une
variante simplifiée.
|
||||||||
|
|
Sommaire de cette page >>> Principe de l'algorithme >>> Exemples |
Débutants Glossaire |
||||||
Anglais: Greedy
algorithm
|
Approche Une fraction égyptienne a généralement l'unité
pour numérateur. Une fraction quelconque est alors représentée par
une somme de fractions de numérateur unité. Fibonacci a imaginé différentes méthodes pour y
parvenir dont l'algorithme dit "glouton". |
|
|
|
Formulation Le procédé est récurrent. Chaque fraction est décomposée en deux fractions
dont la première à un numérateur unité. La seconde est
utilisée pour recommencer le procédé jusqu'à ce que celle-ci possède,
elle-aussi, un numérateur unité. |
|
|
|
|
But Imprimer la suite des fractions égyptiennes correspondant
à une fraction quelconque. Commentaires La boucle est interrompue (break) dès que la seconde fraction a un
numérateur égal à 1 (y = 1). Dans la boucle (for)
la première fraction (a) est calculée;
ainsi que la seconde (b). Les nouvelles valeurs de x et y sont le
numérateur et le dénominateur de b. La suite des fractions est placée dans la liste L
qui est imprimée en fin de programme. |
|
Voir Programmation – Index
|
|
|
||
|
Record de quantité de termes pour les nombres premiers de 3 à 100 en
dénominateur |
|
||
|
Record du dénominateur le plus grand pour les nombres premiers de 3 à 100 en
dénominateur Note: ce mode de calcul des fractions est connu pour engendrer rapidement de
grands nombres au dénominateur (glouton !). |
Uniquement la dernière fraction 50/89,
1/6494499543074890436870241790813851000203090 8/97,
1/57950458706754280171310319185991860825103029195219542358352 93576538994186863423603617986890532737493726150436618102283718985 39583862011424993909789665. |
||
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |