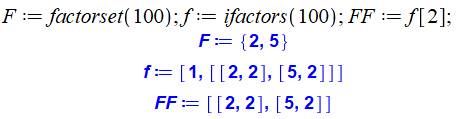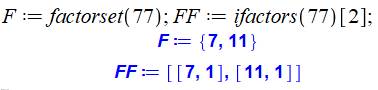|
Édition du: 06/07/2025 |
|
INDEX Nombres
selon facteurs Nombres
selon diviseurs Nombres –
Classification |
Types de Nombres – FACTEURS |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
NOMBRES BRILLANTS
Nombres composés
dont les facteurs comptent tous le même nombre de chiffres. |
||
|
|
Sommaire de cette page >>> Nombres brillants >>> Liste de nombres brillants >>> Programmation – Maple |
Débutants Glossaire |
Anglais: Brilliant number: the product of two primes with the
same number of digits.
![]()
Principaux
nombres selon la quantité de facteurs
|
ak
٠ bl ٠ cm … & ak' ٠ bl' ٠ cm'
… |
|
|
a1
٠ b1 ٠ c1 … |
|
|
a1
٠ b1 |
|
|
a1
٠ b1 ٠ c1 |
|
|
a1
٠ b1 & #a = #b (# est la quantité de chiffres) |
Voir détails en Types
de nombres selon leurs facteurs
|
Famille |
Nombre / Diviseurs / Multiplicatif /
Composé / Famille |
||
|
Approche |
|
2
× 7 = 17 5
× 5 = 25 29
× 71 = 2 059 Ces
nombres sont brillants. |
|
|
Définition |
n = p ٠
q avec quantité de chiffres de p = quantité de chiffres de q. |
||
|
Propriétés |
|
||
|
Anglais |
|
||
|
Les 210 nombres brillants
jusqu'à 5000 |
4, 6, 9, 10, 14, 15,
21, 25, 35, 49, 121, 143, 169, 187, 209, 221, 247, 253, 289, 299, 319, 323,
341, 361, 377, 391, 403, 407, 437, 451, 473, 481, 493, 517, 527, 529, 533,
551, 559, 583, 589, 611, 629, 649, 667, 671, 689, 697, 703, 713, 731, 737,
767, 779, 781, 793, 799, 803, 817, 841, 851, 869, 871, 893, 899, 901, 913,
923, 943, 949, 961, 979, 989, 1003, 1007, 1027, 1037, 1067, 1073, 1079, 1081,
1121, 1139, 1147, 1157, 1159, 1189, 1207, 1219, 1241, 1247, 1261, 1271, 1273,
1333, 1343, 1349, 1357, 1363, 1369, 1387, 1403, 1411, 1457, 1501, 1513, 1517,
1537, 1541, 1577, 1591, 1633, 1643, 1649, 1679, 1681, 1691, 1711, 1739, 1763,
1769, 1817, 1829, 1843, 1849, 1891, 1909, 1927, 1943, 1961, 2021, 2047, 2059,
2077, 2117, 2173, 2183, 2201, 2209, 2231, 2257, 2263, 2279, 2291, 2407, 2419,
2449, 2479, 2491, 2501, 2537, 2573, 2581, 2623, 2627, 2701, 2747, 2759, 2773,
2809, 2813, 2867, 2881, 2911, 2923, 2993, 3007, 3053, 3071, 3127, 3139, 3149,
3233, 3239, 3293, 3337, 3397, 3403, 3431, 3481, 3551, 3569, 3589, 3599, 3649,
3713, 3721, 3763, 3827, 3869, 3901, 3953, 3977, 4087, 4171, 4183, 4187, 4189,
4307, 4331, 4399, 4453, 4489, 4559, 4661, 4717, 4757, 4819, 4891, 4897 |
|
|
|
But Lister les nombres
brillants, les nombres à deux facteurs identiques (carrés) ou distincts. Principe On demande à la fois
la liste des facteurs et la factorisation complète. On compare les valeurs et la quantité des
nombres. Détails
des comparaisons ci-dessous. |
||
|
Carré |
Exemple
pour 100 = 10²:
Test si un seul facteur:
la liste [2, 2] est transformée n ensemble {2}. Il suffit de tester si cet
ensemble ne comporte qu'un seul nombre: nops (F) = 1 Dans le cas des carrés
[2, 2], on passe à l'ensemble, éliminant les redondances: [2, 2] devient {2};
il suffit de tester si cet ensemble ne comporte qu'un seul nombre: nops (F) =
1. Dans le cas de 100:
nops({2, 5}) = 2 nombres. le nombre 100 n'est pas brillant. En effet 100 = 2 ×
2 × 5 ×
5 soit quatre facteurs. On élimine les cas de
puissances supérieures (comme 24) en testant l'exposant du facteur
unique avec FF[1, 2], deuxième nombre de
la liste de factorisation. Il doit valoir 2 pour le seul carré |
||
|
Deux facteurs distincts |
Exemple
pour 77 = 7 × 11
On teste si le jeu de facteurs (F)
compte bien deux nombres (nops(F) = 2). La somme des deux exposants [7, 1] [11, 1]
doit être égal à 2. Les deux nombres doivent être de
même longueur. Calcul de quantité de chiffres avec le logarithme du nombre. |
||
|
Listing pour copier coller dans Maple |
restart; with(numtheory): B := {}:
for n to 50 do F := factorset(n); L := {}; FF := ifactors(n)[2]; if nops(F) =
1 and FF[1, 2] = 2 then B := {n, op(B)} end if; if nops(F) = 2 then kt :=
FF[1, 2]+FF[2, 2]; if kt = 2 then l1 := floor(log[10](F[1]))+1; l2 :=
floor(log[10](F[2]))+1; if l1 = l2 then B := {n, op(B)} end if end if end if
end do: B;
|
||
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Brillant.htm
|
![]()