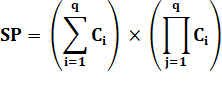|
||||||||||||||||||||||||||||
![]()
|
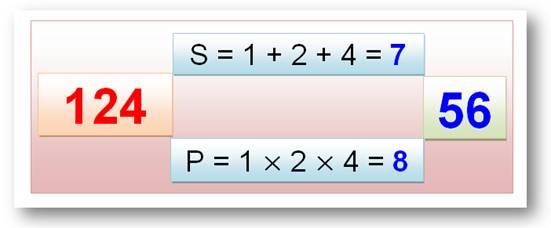
Somme x Produit des chiffres d'un nombre SP Nous
connaissons la somme des chiffres et le produit des chiffres. Et si nous les multipliions? Ici, nous garderons les calculs originaux
sans recourir à des itérations dans un premier temps. Les
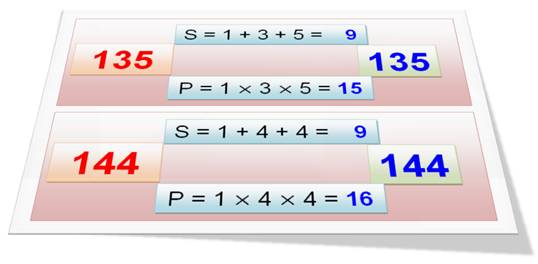
cas intéressants sont ceux pour lesquels le nombre serait égal
au produit SP. Cela n'arrive que pour 135 et 144. |
Anglais:
Sum-Product
numbers
|
|
|
|
Qui
se lit:
le
nombre "somme fois produit" (SP) est égal à la somme de tous les
ièmes chiffres pour i de 1 à q (quantité de chiffres) multipliée par le
produit de tous les ièmes chiffres pour i de 1 à q.
Ex
12 21 |
|
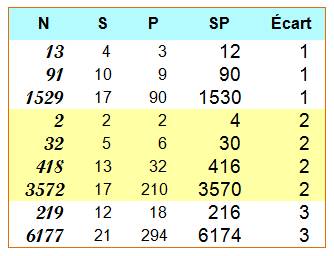
Exemples
pour les nombres de 0 à 99
(En rouge les nombres en double)
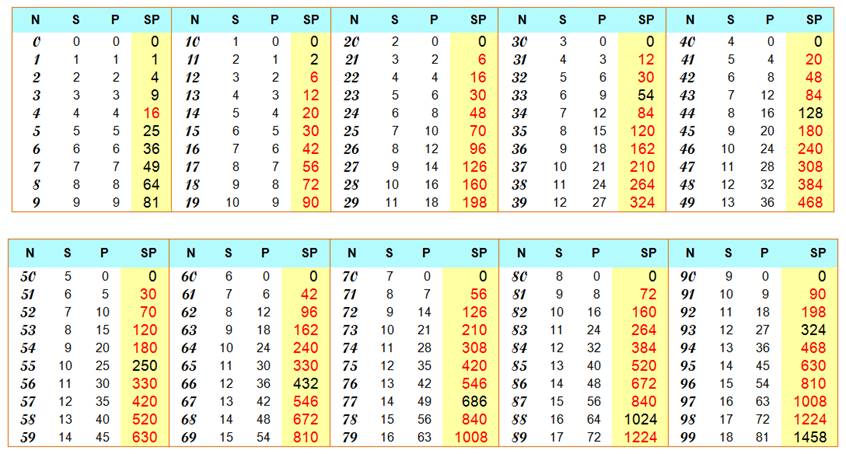
|
|
|
|
Notez
que S(144) = 9 = 3² et P(144) = 16 = 4². Deux carrés. |
|
Voir Nombre = Somme des chiffres de nk + Produit
des chiffres de nh
|
|
|
|
Exemple
On note: 132, 36,
162, 108, 0 Autres exemples 0, 0 1, 1 2, 4, 16, 42,
48, 384, 1440, 0
(6 cycles) 3, 9, 81, 72, 126, 108, 0 4, 16, 42, 48, 384, 1440, 0 5, 25, 70, 0 6, 36, 162, 108, 0 7, 49, 468, 3456, 6480, 0 8, 64, 240, 0 9, 81, 72, 126, 108, 0 10, 0 11, 2 … (7 cycles) 88, 1024, 0 115, 35, 120, 0 114, 24, 48, 384, 1440, 0 111, 3, 9, 81, 72, 126, 108, 0 567, 3780, 0 789, 12096, 0 123456, 15120, 0 92, 198, 1296, 1944, 2592, 3240, 0 999, 19683, 34992, 52488, 69120, 0 9996, 144342, 6912, 1944, 2542, 3240, 0
Exemples 1, 1 332, 144, 144 … 89, 1224, 144, 144 … 139, 351, 135, 135 … Suite en Table des nombres SP en itération
11, 2, 4, 16,
42, 48, 384, 1440, 0
12 avec 4 itérations. 13 avec 5 111 avec 6 36 699 avec 7; jeu égal avec 11. 1 233 699 le suivant avec 7 itérations. 3 777 788 avec 8. 11 138 888 suivant avec 8. Aucun autre jusqu'à cent millions.
3 777 788, 21 666 624, 684 288, 884 736, 1 161 216, 1
296, 1 944, 2592, 3 240, 0. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
|
![]()