|
|||||||||||||||||||||||||||||||||||
![]()
|
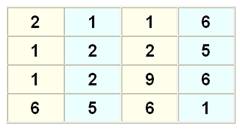
CARRÉS MAGIQUES DE CARRÉS Les
chiffres lus verticalement comme horizontalement forment des carrés parfaits.
|
|
|
|
|
Il s'agit de construire un carré avec des nombres
carrés de deux chiffres. En bilan, ol est possible
de lire des carrés en horizontal comme en vertical. Carrés à deux chiffres: 16, 25, 36, 49, 64 et 81. Quatre cas satisfaisants:
|
|
|
Il s'agit de construire un rectangle avec deux nombres carrés
de trois chiffres. La lecture verticale donne également des carrés. Carrés à trois chiffres: 100, 121, 144, 169, 196, 225,
256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 800,
961. Dans le rectangle, la ligne du bas est celle des unités
des carrés lus verticalement. Or, un carré se
termine par: 0, 1, 4, 5, 6 ou 9. Le nombre du bas ne comporte
exclusivement que ces chiffres. Ne restent que les nombres: 100, 144, 169, 196, 400,
441 et 961 comme possible en position basse. Seule possibilité:
|
|
Pour la recherche des solutions, on remarque le carré
du bas, de même que le carré de droite, ne doit contenir que des 0, 1, 4, 5,
6 ou 9, car ce sont des unités de carrés. Puis, on utilise les propriétés du chiffre des dizaines
d'un nombre carré selon le chiffre des unités. Treize solutions:
Si on tolère les zéros initiaux, il y a 32
solutions en plus. Si, de plus on admet 000 comme un carré, il
y a 45 combinaisons de plus. |
|
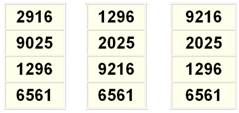
Une seule solution, si on exclut le chiffre zéro:
Si on admet le zéro, mais pas en position initiale,
alors on a 12 solutions de plus. Par exemple, les trois suivants qui, de plus
présentent une étrange similitude:
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/CarMagCa.htm |
![]()