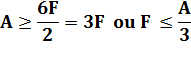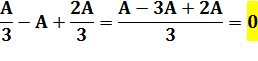NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/10/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TOPOLOGIE
Débutants Géométrie	QUATRE COULEURS						Glossaire Géométrie
INDEX Quatre couleurs Géométrie Topologie	2 couleurs	3 couleurs		4 couleurs	5 couleurs	6 et plus
			Sommaire de cette page >>> Certains cas se résolvent facilement >>> Cinq ou quatre couleurs >>> Difficultés et impossibilités >>> Théorème de De Morgan >>> Cinq voisins >>> Quatre ou cinq ? >>> Théorème des cinq couleurs >>> Méthode de réduction >>> Au moins une région avec cinq arêtes

Cas de CINQ COULEURS

En voulant démontrer les quatre couleurs, Kempe avait finalement réussi à démontrer le cas de cinq couleurs.

Certains cas se résolvent facilement
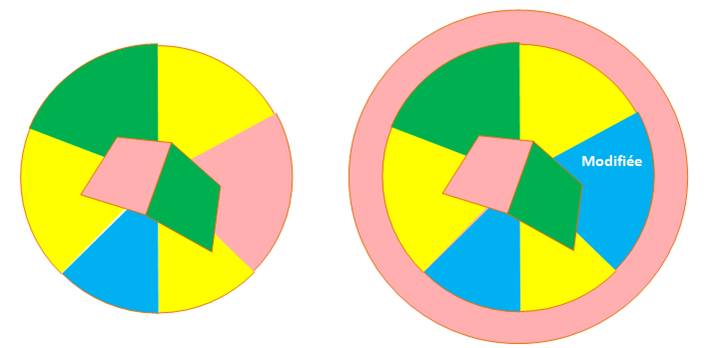
La carte est colorée avec quatre couleurs, la région suivante entoure les quatre. Comment faire? Ici, il est possible de modifier l'une des couleurs.

Cinq couleurs ou quatre

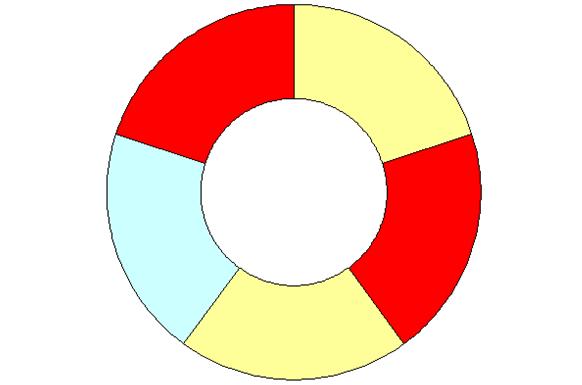
Colorier une carte quelconque avec cinq couleurs est toujours assez facile. Un exemple permet de toucher du doigt la difficulté de démontrer que quatre est suffisant. Soit le dessin suivant  Cet exemple illustre le fait que: il n'existe pas de configurations pour lesquelles chacune des cinq régions partage une frontière commune avec les quatre autres. Nombreux sont ceux qui ont conclu à tord que, puisque cinq régions ne pouvent jamais être adjacentes aux quatre autres, alors quatre couleurs suffisent. Conclusion Le nombre de couleurs n'est pas égal au plus grand nombre de régions adjacentes. On ne peut pas utiliser une telle implication, même si à première vue, elle paraît évidente. La démonstration devra utiliser de nombreux artifices pour déjouer ce piège, et pour arriver à quatre couleurs, il faudra examiner des milliers de cas possibles par ordinateur.

Difficultés et impossibilités
Il est possible de construire un graphe avec six sommets, chacun peut être relié à trois autres. Par contre, il est impossible de construire le même graphe mais avec cinq sommets, chacun relié à trois autres.
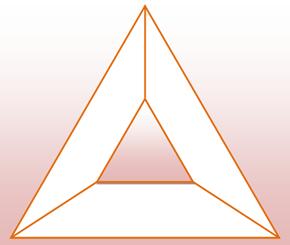
Difficulté pour construire cinq régions chacune voisine des quatre autres Graphe avec six sommets, chacun raccordé aux cinq autres, sans croisement. Impossibilité démontrée par De Morgan.
Difficulté de trouver cinq régions avec frontières communes Pour introduire la cinquième, il faut passer dans l'une des quatre autres.

Théorème de De Morgan
Théorème Il est impossible de disposer cinq régions de telle façon qu'il existe des frontières communes entre tous les couples possibles. Ou, aussi Il n'existe aucune carte avec cinq pays, chacun jouxtant les quatre autres. Ou, équivalent Il n’existe pas de graphe à cinq sommets de sorte que chaque sommet soit connecté aux cinq autres sans branches qui se coupent. Illustration La diagonale rouge coupe l’autre diagonale	Démonstration Un truc pour commencer On ajoute une région au graphe, la région externe. La relation d’Euler devient: F – A + S = 2 Or, ici S = 5 A = 4 + 3 + 2 + 1 = 10 Avec la relation d’Euler, le nombre de régions doit être F = A – S + 2 = 7 Deuxième évaluation Chaque région est limitée par au moins trois arêtes. Soit, avec la conclusion précédente, le graphe compte au moins: 7 x 3 = 21 arêtes. Chaque arête limite deux régions. On a donc compté les arêtes deux fois. Il faut diviser par 2: A > 21/2 A 11 (Il n’y pas de ½ arête) Contradiction On avait calculé seulement 10 arêtes et non 11. L’hypothèse de départ est fausse Il n’est pas possible de connecter cinq points sans recoupement.

Voir Lois de De Morgan en logique

Cinq voisins
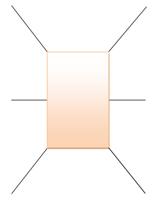
Toute carte contient au moins un pays qui à cinq voisins ou moins. Supposons une région avec six voisins. Un calcul arithmétique avec la relation d'Euler montre que ce n'est pas possible. Démonstration	Exemple de région avec six voisins Forme complète et forme simplifiée
Chaque sommet reçoit au moins 3 arêtes, et chaque arête connecte deux sommets.
Supposons que la carte ne comporte que des régions à six frontières ou plus.	F régions (ou faces) avec plus de cinq frontières.
Si toutes les régions avaient six arêtes (cas minimum), chaque arête bordant deux régions.
En injectant ces valeurs dans la relation d'Euler avec les valeurs minimales	F – A + S = 2
L'invariant d'Euler n'est pas respecté	La contradiction montre que la carte de peut pas ne contenir que des régions ayant six régions ou plus.

Démonstration alternative (même principe)

Le passage d'une carte quelconque à une carte normale (3 arêtes par sommet) s'effectue sans grande difficulté. On montre qu'il faut le même nombre de couleurs pour l'une et pour l'autre. Ainsi, s'il existe une carte quelconque à cinq couleurs, alors elle peut être simplifiée en une carte normale à cinq couleurs (CNCC).
Pour une CNCC, chaque sommet limite trois régions:	s = 2a / 3
Relation d'Euler:	s – a + f = 2 devient: 3f – a = 6
Si Pn est le nombre de pays qui possède exactement n frontières, et N est le plus grand nombre de frontières parmi tous les pays, alors: La formule commence par 2 car pas d'enclaves, ni d'îles.	f = P2 + P3 + … + PN e = ½ (2P2 + 3P3 +… + N.Pn)
En combinant les deux relations:	4P2 + 3P3 + 2P4 + P5 – P7 – 2P8 – 3P9 – …– (N – 6)PN = 12
Cette somme algébrique est positive. Or Pn est positif ou nul.	Pn contribue positivement à la somme que si n vaut 2, 3, 4 ou 5.
Ce qui veut dire que l'une de ces quatre valeurs au moins est positive et non pas toutes nulles. Autrement dit: si une carte est normale, il existe au moins un pays qui sera entouré de 2, 3, 4 ou 5 pays.

Théorème des cinq couleurs
Théorème de Heawood (1890) Cinq couleurs suffisent toujours pour colorier une carte sans région adjacentes de la même couleur. Procédé de réduction Il faut trouver un procédé qui n’altère pas le nombre maximum de couleurs. On a dénombré un total de 6 cas. Intérêt Donner un résultat tangible avec une preuve courte.	Démonstration On utilise encore le même truc. Il y a une région extérieure au graphe. ou autrement dit: On imagine le graphe dessiné sur une sphère. Alors: F – A + S = 2 Méthode On va réduire les régions de la carte de départ (quelconque) en associant deux régions adjacentes. Et, ceci pour aboutir à un graphe final de cinq régions seulement. Ainsi Le graphe final nécessite cinq couleurs, au plus.

Voir Démonstration / Historique

Méthode de réduction – Principe
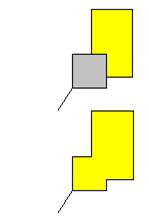
Cas 1		Dans toute la suite, on suppose que le reste de la carte est résolu et que subsiste ce type configuration. Valable pour toute la description ci-dessous. Ici, on fusionne la partie intérieure. Bilan (évident), il faut deux couleurs.
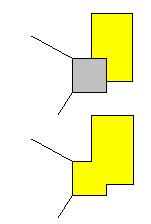
Cas 2		Sommet avec plus de trois arêtes. Soit pus de quatre régions. Il existe une paire de régions qui n'a pas de frontière commune. Elles fusionnent. On donne la même couleur à cette nouvelle région. Tout coloriage initial de la carte n'est pas modifié par cette opération. En appliquant cette procédure, les sommets comportent au plus trois arêtes.
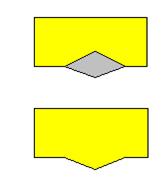
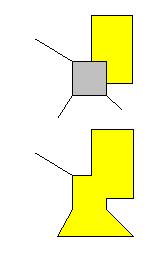
Cas 3		Région limitrophe avec deux autres. On la fusionne avec l'une des deux. Si on peut colorier la carte avec au moins trois couleurs, la nouvelle carte pourra, elle aussi, être colorié avec trois couleurs. La partie "engloutie" sera coloriée différemment des deux régions l'entourant.
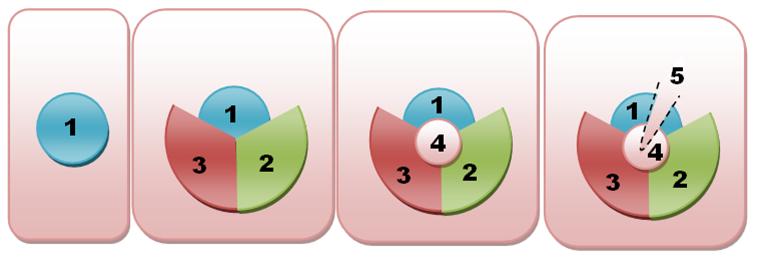
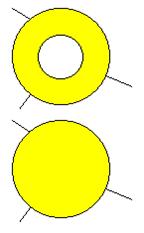
Cas 4		Une région avec trois voisins. On fusionne avec l'un d'entre eux. Si la nouvelle carte peut être coloriée avec quatre couleurs, la carte d'origine peut l'être aussi.
Cas 5		Une région avec quatre voisins. On fusionne avec l'un d'entre eux. Si la nouvelle carte peut-être coloriée avec cinq couleurs, la carte d'origine peut l'être aussi.

En appliquant ces trois derniers procédés, une région est entourée par au moins cinq autres (Le cas n° 6 sera examiné plus tard).

En appliquant tous ces procédés de réduction

On aboutit à une carte avec:

aucune zone entourée;

chaque sommet comporte trois arêtes; et

chaque région à au moins cinq arêtes.

On va montrer que cette nouvelle carte possède, au moins, une région de 5 arêtes (bordures).

Région à six arêtes en moyenne

Soit a le nombre moyen d’arêtes bordant une région.

Nombre total d'arêtes: A = a. F

Sauf que: Une arête borde 2 régions: A = a. F / 2

Chaque sommet reçoit 3 arêtes.

Nombre de sommets: S = A / 3

Sauf que: Une arête aboutit à 2 sommets: S = 2 . A / 3

Déduction et calcul de la relation d'Euler

3S = 2A = aF

V = 1/3 aF

E = 1/2 aF

1/3 aF – 1/2 aF + F = 2

a = 6 – 12/F

=> a < 6

Le nombre moyen d'arêtes est inférieur à 6

Or, nos réductions successives aboutissent à des régions dont le nombre de frontières est au moins cinq. Pour obtenir une moyenne inférieure à 6, il en faut au moins une à 5.

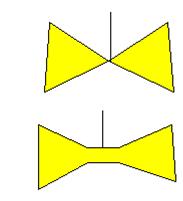
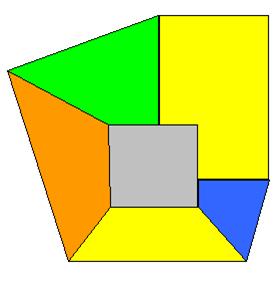
Cas 6		Une région avec cinq voisins. Il existe une paire de régions qui ne se touchent pas. On fusionne les trois. Si la nouvelle carte peut-être coloriée avec cinq couleurs, la carte d'origine peut l'être aussi. Il faut quatre couleurs pour la nouvelle carte: trois pour l'extérieur; une pour la région fusionnée (jaune, ici). On dé-fusionne en donnant la 5^e couleur à la région centrale et en gardant le jaune pour les deux régions séparées.
Bilan		Note Inutile d'optimiser à moins de cinq couleurs Le cas n° 5 de réduction impose les cinq couleurs.

Retour Suite	Cas de six couleurs ou plus Théorème des quatre couleurs Quatre couleurs – Index
Voir	Cinq pays Couleurs Démonstration Énigme des carrés mitoyens Graphe à 2 couleurs Indicateur d'Euler-Poincaré Introduction à la topologie Quadrichromie Topologie – Glossaire Topologie – Index
DicoNombre	Nombre 4 Nombre 5
Sites	Voir références
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Coul5.htm