|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Théorèmes des QUATRE COULEURS Après avoir cerné le nombre
de couleurs nécessaire pour colorer une carte plane, nous avons montré que 3 n'est pas suffisant et que 5 est
toujours suffisant. Montrer que 4 est suffisant fut une grande épreuve.
La démonstration avec l'aide d'ordinateurs date de 1976.
|
|
|
|
|
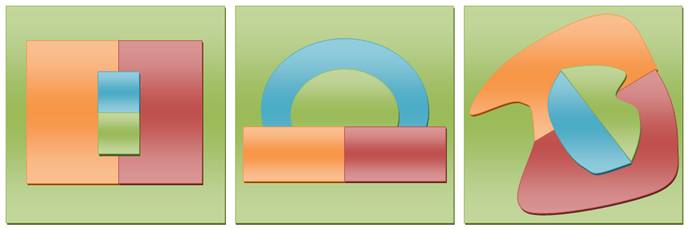
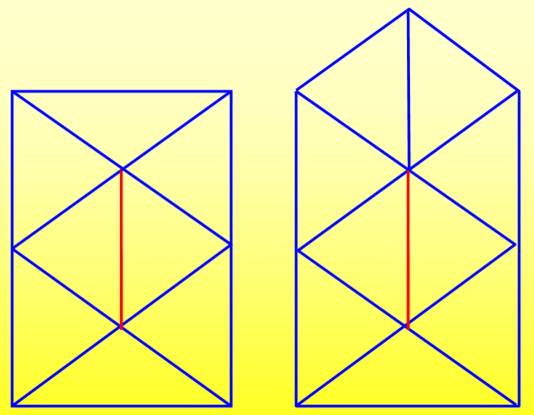
Il faut quatre couleurs dès qu'une région
est entourée d'un nombre impair de régions
Point multiple impair: trois couleurs Régions limitrophes
impaires: quatre couleurs En 1898, Heawood
démontre que si le degré de tous les sommets est divisible par 3, alors la
carte est 4-coloriable. Situation Dans tous les cas quatre couleurs
suffisent. Le théorème des quatre couleurs fut démontré en 1976 par Kenneth
Appel et Wolfgang Haken sur ordinateur qui calcula
pendant 1200 heures pour réussir à établir le résultat. Plus tard (1997 ?), Neil Robertson,
Daniel Sanders, Paul Seymour et Robin Thomas ont
refait et simplifié la preuve de 1976. Aucune des deux n'est assez simple pour
être vérifiée à la main, mais le théorème des quatre couleurs est tout de
même considéré comme définitivement acquis. |
|
|
|
|
|
|
|
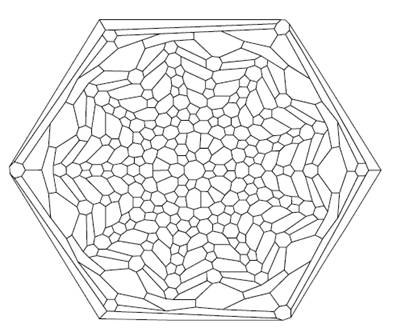
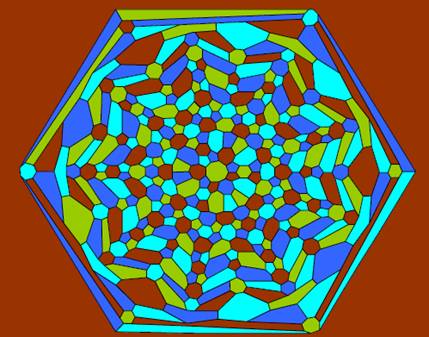
Exemples
de configurations étudiées

|
|
|
|
|
|
|
|
|||||||||||||
|
Suite aux travaux de Kempe, on sait que:
une triangulation qui représente une carte
minimale à cinq couleurs ne peut pas avoir de sommets
avec moins de cinq arêtes. Astucieusement Heesch
opère une analogie électrique en associant le graphe à un circuit électrique dont il
va chercher à équilibrer les charges. Il donne les charges suivantes aux
sommets:
La somme des charges dans tout le circuit est
positive (en fait égale à 12, valeur déduite de la relation d'Euler). On va
redistribuer les charges autour de 0, tout en conservant la somme. Le truc consiste à trouver une méthode de
redistribution équilibrant les charges et finissant par des configurations
limites, avec impossibilité d'aller plus loin. La somme totale étant positive, il y aura
toujours des sommets positifs. Pour le graphe, la charge totale est toujours
exactement égale à 12. Ce qui veut dire que la charge du graphe est toujours
positive. Une charge est affectée à chaque sommet. Elle est
égale à 6 – d, avec d le degré du sommet. Les sommets de degré supérieur à 6
sont donc négatifs, ce sont les sommets majeurs. Et seuls les sommets de
degré égal à 5 sont positif (+1). L'idée est d'écouler les charges positives vers
les négatives des sommets majeurs, à charge totale conservée. Le but est de
mettre en évidence les nouvelles charges positives qui correspondraient à des
configurations réductibles. Comme toute triangulation doit posséder des
sommets de charges positives, les configurations mises en évidence par ce
procédé doivent former un ensemble inévitable. Exemple Tous les sommets de charge 5 donnent 1/5 à tous
les sommets voisins de charge > 6. Alors, deux configurations inévitables subsistent:
|
|||||||||||||
|
|
||||||||||
|
Les
procédures de réduction par les charges
s'améliorent. En 1970, Haken en réduit encore le nombre.
Néanmoins, le volume de calcul pour les explorer toutes est énorme; mais,
cela commence à être accessible. En 1972, Wolfgang
Haken et Kenneth Appel travaillent ensemble et
affinent la procédure par approches d'améliorations successives. Trois ans de
travail, 500 modifications plus tard et avec 1200 de calcul… … En juin 1976 L'analyse
de tous les cas est terminée et le théorème des quatre couleurs démontré. En 1995 Nouvelle
démonstration, plus simple, mais dans la même veine par Neil Robertson, Sanders, Seymour et Thomas.
Le
théorème est démontré, mais la question du coloriage des cartes fait toujours
l'objet de recherches intenses. |
||||||||||
Voir Historique complet
Monstre!
|
La
démonstration repose sur l'analyse d'environ
2000 cartes particulières où l'on montre que chacune d'elles se
comporte d'une certaine manière. La vérification de tous les cas particuliers
est une tâche fastidieuse, qui a demandé plusieurs milliers d'heures de
calcul sur ordinateur puissant. Si l'on devait rédiger cette démonstration in
extenso, le texte en serait si monstrueux que personne ne vivrait assez
longtemps pour le lire intégralement, et à plus forte raison pour le
vérifier. Ian
Stewart – Les mathématiques - Page 118 |
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Les
premières pages sont consultables
en e-book
|
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Coul4.htm
|
![]()